武蔵中の算数分析（2016年）

受験者平均点　48.6 点

合格者平均点　68.1 点

想定合格点　　60 点

武蔵中学の学校の特徴や傾向分析、2018年の分析はこちら

答案例はこちら

大問1

(1)　〇

「分数と分数をかけて整数になる」というのは、約数・倍数の典型題ですね。

今回は分数の割り算の話ですが、根本は同じです。

確実に正解しておきましょう。

(2)　〇　〇

平面図形と相似の典型題です。

平行四辺形の向かい合う辺の長さが等しいことを利用し、AD＝BC＝㊵として考えましょう。

こちらも確実に正解しておきたい問題です。

大問2

(1)　〇

食塩水のやり取りの典型題です。

BからCに食塩水を移しても、Bの濃さが変わらないことに気づけば易しいでしょう。

(2)を正解するためにも、丁寧に整理しておきましょう。

(2)　×

「AとCの食塩水の濃度が等しい」ことと「Aの食塩水は400g、Cの食塩水は500gになった」ことから、「AとCに含まれる食塩の量の比は4:5になった」と言い換えましょう。

あとは解答例のように消去算に持っていけば良いでしょう。

やや難度の高い問題です。

大問3

(1)　△

女子は3÷4.5＝2/3時間＝40分歩いたことが分かります。

車は学校からAまでに3÷45＝1/15時間＝4分と、乗り降りに1分かかるので、AB間の往復には40-4-1＝35分かかります。

あとは速さと時間の逆比を利用しましょう。

(2)　△

(1)の続きとして、答案例のように女子がA地点を出発してからの旅人算と考えましょう。

女子の乗り降りの1分の足し忘れに気を付けましょう。

(3)　△

さらに(2)の続きです。

(2)で追いついた地点を起点として、速さと時間の逆比を利用しましょう。

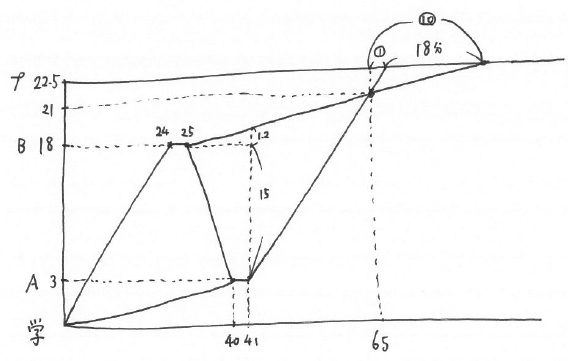
なお今回の解答例では、条件を線分図で整理しましたが、「複数の点が行ったり来たりする」というテーマなので、以下のようにダイヤグラムで整理することも効果的です。

大問4

(1)　〇

題意の確認問題です。

確実に正解しましょう。

(2)　△

「3個のカタマリを出来るだけ多く作る」という方向で考えましょう。

きちんと題意を把握していれば、決して難しくはない問題です。

(3)　△

得点を和分解して考えましょう。

4＝1＋1＋1＋1もしくは1＋3(＋0)

9＝1＋1＋1＋3＋3

11＝1＋1＋3＋6

〇が7個になるよう気をつけて、丁寧に処理しましょう。

この出題で合格点の60に乗せる方法を考えてみましょう。

・大問1を完答

・大問2(1)を正解

・大問4で半分は得点

まずは、これで約50点。

あとは大問3で得点を積み上げるか、大問4を完答に近づけるかで合格点を越えることが出来るでしょう。

2016年の出題では、確実に正解すべき問題が明確だったので、大問3の得点が合否を分けたと言うことが出来そうです。

ただこれは全ての問題に充分に目を通すことが出来た場合の話です。

大問2と大問3で時間をつかいすぎて、決して難しくない大問4に充分な時間を割くことが出来なかった受験生も少なからずいたものと考えられます。

時間配分や問題の取捨選択と言ったテスト戦略も、過去問演習を通して確立していきましょう。