この記事を書いたのは...
松田 浩志
自律学習サカセルでは算数・国語、主要2科目を担当。
大手進学塾では、教務主任職として、校舎全体の運営を担当し、日曜日の志望校別コースの最上位クラスから自校舎の基本クラスまで、算数・国語の両科目で毎年幅広くクラスを担当してきた。
現在の趣味はファッション。
もともと古着が好きだったのですが、現在は「キレイめ」なファッションが好み。
個別指導・家庭教師の自律学習サカセル
サカセルコラム
SAPIX新6年4月マンスリーで押さえるべきポイント!算数編【後編】 Column

4月マンスリー確認テスト 算数 各単元のポイントについての解説の後編です。
前編はこちらからご覧ください。
関連記事:SAPIX新6年4月マンスリーで押さえるべきポイント!算数編【前編】
【仕事系の問題 (仕事算)】
マンスリーテストでも毎年のように大問や小問として出題されており、必ず出来るようにしたい単元です。
・「時間のヒント」→「時間の比」→「仕事の速さの比」という動きが出来ている
・「速さの比」×「時間」で「全体の仕事量の比」を出せることを理解している
・「全体の仕事量の比」÷「速さの比」で「時間」が出せることを理解している
基本になります。しっかり解けるようにしましょう。
「時間のヒント」→「時間の比」→「仕事の速さの比」という動きが出来ているか確認しましょう。
また、全体の仕事量を比で出してしましましょう。
自分は表にまとめて整理させて指導をしています。
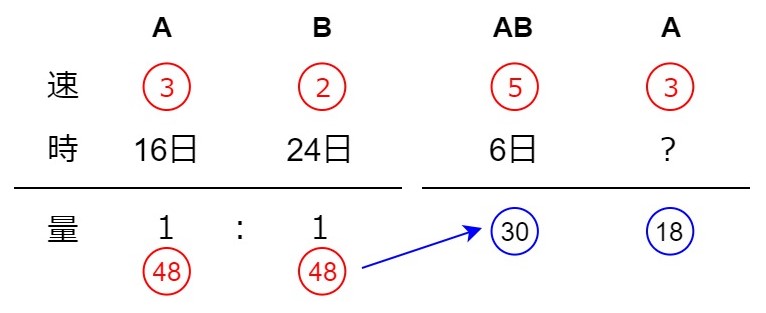
3人のパターンはマンスリーテストでも頻出です。最低限、仕事の速さの比までは確実に出せるようにしておきましょう。連比を利用します。
(1)これは速さの比が出てしまえば非常に簡単です。
(2)A:Bの仕事の速さがそのまま仕事量になることを理解しているか確認しましょう。速さの問題で出てくる「速さの比」から「距離の比」を出すのと同じ発想です
「休んだ分の仕事量」=「多く働く分の仕事量」で等式が立てられます。
そして、この式から比を出していきます。
まずは、式が立てられているか確認し、そこから比を出せているか確認しましょう。
比さえ出てしまえば、あとは簡単です。
上記のD1やC4と似た発想です。
式を立てられるかどうかの確認とそこから比を出せるかの確認をしましょう。
仕事の速さの比が出てしまえば、あとは基礎と同じ流れですね。
D1やD2と同じ発想の問題です。
ヒントから等式を立てて、比を出します。D1やD2と比べて少し複雑なのが難しい点ですが、しっかりとまとめていけば問題ないでしょう。
速さの比さえ出てしまえば、あとは同じ流れです。
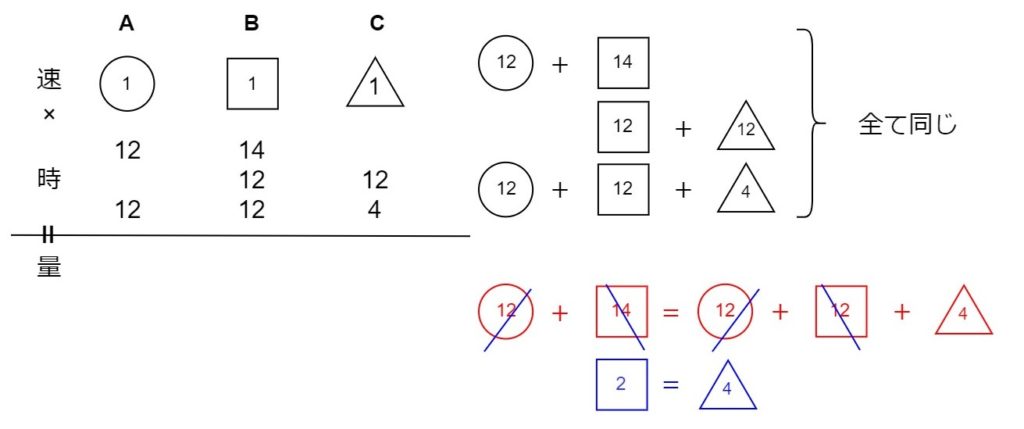
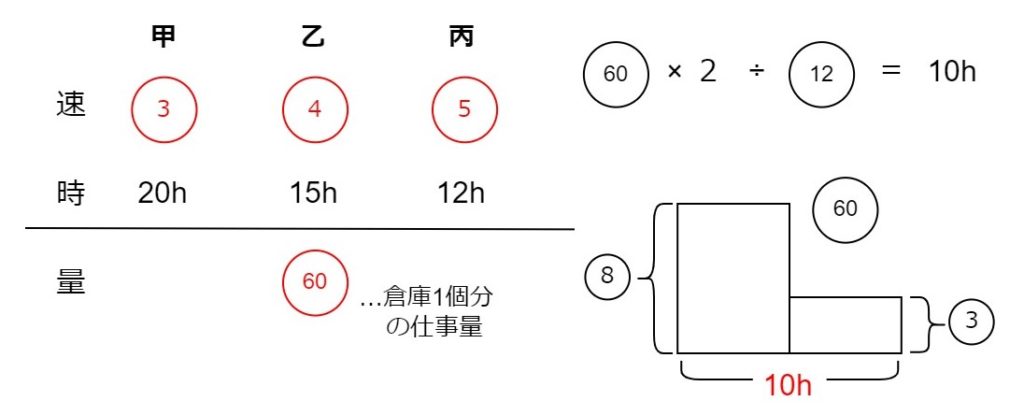
先述しましたが、3人のパターンの仕事算はマンスリーテストでも頻出です。しっかりと解けるようにしておきましょう。
仕事の速さの比はすぐに出せると思います。そして、「途中から速さが変わる」のでつるかめ算を利用すると分かります。まずはここを確認しましょう。
次に、つるかめ算をするためには時間が必要です。ここで「倉庫1つに対して甲と丙が協力して仕事をしている」という発想から「倉庫2つに対して甲と乙と丙の3人で協力して仕事をしている」という発想に切り替えます。この考え方が出来ているか確認しましょう。
【割合を利用した問題 相当算 その他】
基本の問題となります。
日本語を正確に図や式に書き換えていきましょう。一文ずつ分けて、丁寧に作業をしていけば苦手なお子様でも大丈夫です。
「全体の」と「残りの」を読み間違えないように注意しましょう。
バケツの重さも考慮に入れる問題です。12.8kgというヒントと3.8kgというヒントがあり、それぞれ式が立てられることから、倍数算を利用すると判断出来ます。
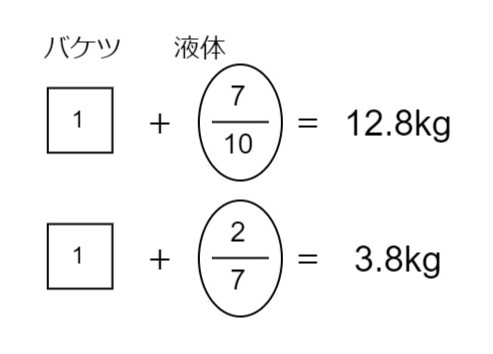
式を立てるのは難しくないと思います。
カップの容積と何杯という数がごちゃごちゃになると比が逆になります。しっかりとお子様に説明させてみて、分かっているか確認しましょう。
A、B、Cの誰を①と置いて(基準として)計算するかが問われています。
式を立ててみてから考えると分かりやすいです。
今回はAを①と置くと分かりやすいです。
Bを①と置くとAを出すのに困ります。Cを①と置くとAとBを出すのに困りますね。
また、括弧の計算が出来ているかも確認しておきましょう。
例えば、(②+3)×4が⑧+12と計算できているかどうかなどです。3×4を忘れないように注意しましょう。
【やり取りをする問題 (やりとり算)】
・図をしっかりとかくことが出来る
やり取りの問題はとにかく図をしっかりかき切ることです。食塩水などでも登場しますね。
横にかく派と縦にかく派の方がいますが、お子様自分の分かりやすい方で良いと思います。
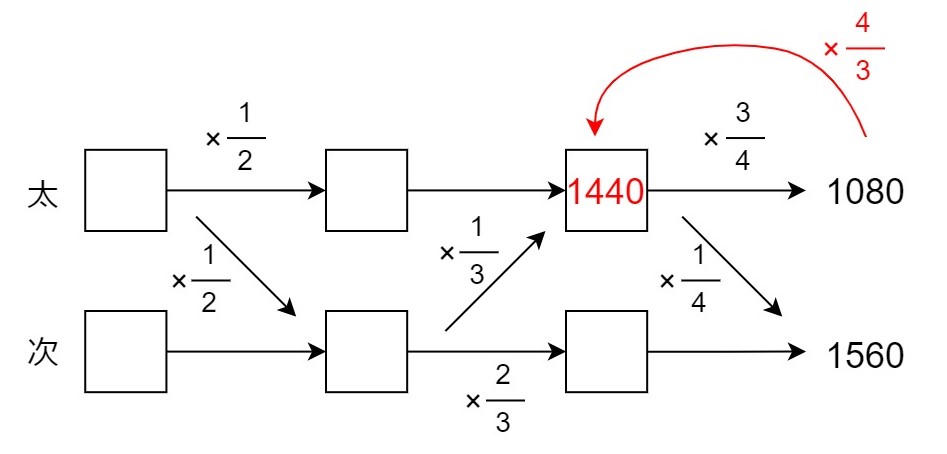
やり取りの中で多くのお子様がこんがらがるのがこのE3の問題です。
払った分のお金を先にかき、そこから同じ金額になるように調整していく図をかくと分かりやすいかと思います。
入試でもマンスリーテストでも見かけないので、そこまで熱を入れてやる必要はないかと思います。
【面積を求める】
・全体から余計な部分を引いて面積を求める発想が常にある
・補助線を引き、分割することで面積を求める発想が常にある
・移動して、面積を求める発想が常にある
・面積比を利用する発想が常にある
基礎になります。しっかり出来るようにしましょう。特に苦手な方はBASICで練習をしておきましょう。
A2の「面積が等しい」の発想は大切なので、おさえておきましょう。AとBが等しい場合、共通の部分を決め、「A+共通の部分」=「B+共通の部分」という形で考えます。これは「面積が等しい」のパターンや「面積の差」のパターンでも登場するので、おさえておきましょう。
A3は2020年と2023年のマンスリーテストで出題されています。
斜線部分を分割する方法もありますが、全体から引くやり方の方が楽かと思います。
斜線部分の1番長い辺の長さが出せることと、直角二等辺三角形の斜辺から面積が出せるかどうかの確認をしましょう。
台形の面積比を覚えているかどうかと、なぜそうなるのかの理屈を確認しましょう。
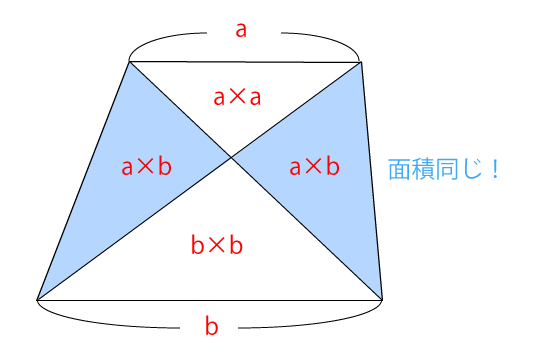
底辺を中に置く発想です。しっかりと確認しましょう。この発想は立体図形でも登場しますので、この機会におさえて置くと良いかと思います。
面積の差を求める問題です。面積の差を求めるときの発想として「片方と同じ面積の部分を見つけor作り、打ち消す」という考え方があります。よく出てくる発想なので、おさえておきましょう。
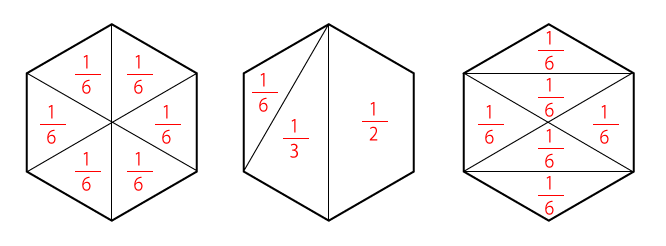
六角形の分割の問題です。分割の方法はいくつかありますので、有名どころは頭に入れておきましょう。今回の問題では「同じ形を作る」という発想を思いつければ覚えていなくても解けますね。
また、六角形は分割で解くパターンと角出しで解くパターンがあります。ここもおさえておきたいですね。基本方針としては「頂点から線が引かれている場合は分割」「頂点から引かれていない場合は角出し」と覚えておくと良いです。もちろん例外はあります。今回もその例外のひとつです。もちろん角出しでも解けます。
「面積の差」のパターンですね。D1とは違い、「共通の部分」を利用した解法です。発想はA2の問題と同じです。「三角形FAD+三角形ABF」−「三角形FEB+三角形ABF」で考えましょう。
また、台形の上底と下底の比を利用した面積比の利用も問われています。こちらもおさえておきましょう。
相似の利用です。相似であると気がついてさえしまえば難しくないかと思います。
また、B3で出てきた直角二等辺三角形の斜辺から面積を出す方法も登場しています。
(1)は簡単なのでぜひ取り組みたいですね。
(2)は論理的な思考が求められる問題です。
「台形の面積を求める」
→「辺BCの長さが必要」
→「三角形ABDの面積が必要!」
→「四角形ABED−三角形BED」
→「四角形ABED=三角形ABE+三角形AED」
という流れですね。
上から3つ目と4つ目の発想がなかなか思いつかないかもしれません。大問形式なので(1)を使って(2)を解くという視点が持てると、少し解きやすくなるかと思います。
【角度を求める】
A1タイプの四角形(ブーメラン型・A型・海パン型・キツネ型などなど)は知識として覚えておきましょう。
B4も知識です。多角形の公式などの知識が覚えられているか確認しましょう。
折り返しの問題です。お子様によってはC2の方が簡単と思われる方もいるでしょう。
折り返しでは折り返す前と折り返した後の図形は合同であるということが使えているか確認しましょう。
また、折り返しでは、折り返す前の図形がかかれていない場合などもあります。この場合は自分で折り返し前の図をかくということも覚えておくと良いでしょう。
(1)は周りの長さの問題です。なぞらせてみて、確認しましょう。また、3.14を最後にまとめて計算しているかも確認しましょう。2023年のマンスリーテストでこの問題の類題が出題されています。
(2)は補助線を用いて、正三角形が見つけられるかが重要です。ここが見えているかどうかを確認しましょう。「困ったときの正三角」は覚えておきましょう。
円の問題での補助線は「中心から円周上への半径」であることがほとんどです。「困ったときの円周上の点に線を引く」も覚えておきましょう。
円の折り返しの問題です。
(1)中心から円周上の点に線を引くという発想と正三角形を作るという発想の組み合わせです。少し難しいと思いますが、おさえておきましょう。
【その他】
忘れているお子様もいると思いますので、線対称と点対称の理解をこの機会に再度しましょう。
(1)長さの差の問題です。D1と似た発想です。「片方と同じ長さの部分を見つけ、打ち消す」という発想です。この発想ができているか、まずは確認しましょう。
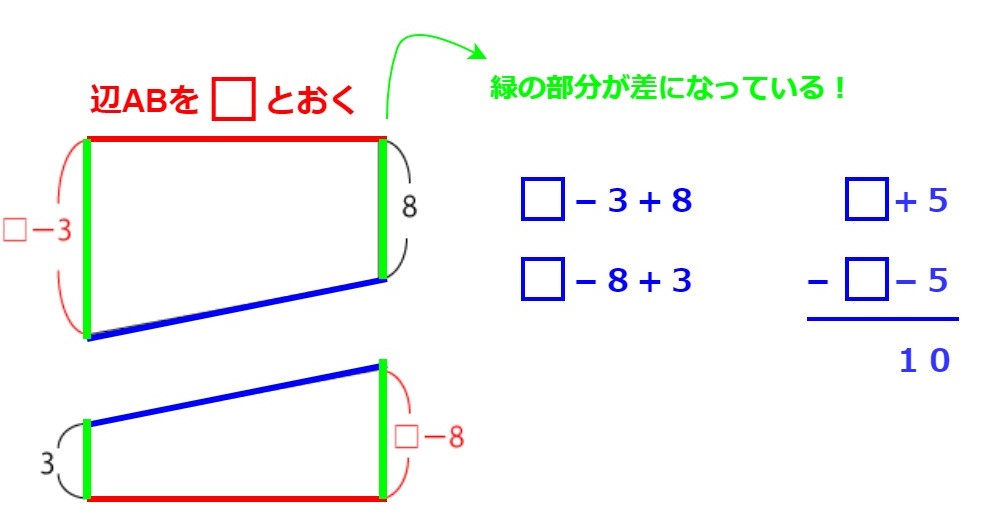
(2)は面積の比を利用する問題です。「上底+下底」が②:①になっています。この利用を思いつけているかまずは確認しましょう。
次に、(1)より、長さの差である「上底+下底」の差が10㎝であるということを踏まえると解けるかと思います。(1)を利用するという発想は度々登場していますね。入試でも模試でも必要な考え方なので、しっかりと頭に入っているか確認しておきましょう。
(3)GDの長さのヒントが出ていることから、DEに補助線を引くという発想が思いつくでしょうか。GDのヒントが出ていなくてもDEに補助線を直感的に引きたいと思える方は慣れているかと思います。四角形を三角形に分ける補助線は補助線の引き方の典型的なパターンですのでおさえておきましょう。
ここから三角形AEDと三角形DEFの面積の比と三角形AEGと四角形EFDGが①:①であることを利用して解きましょう。
立体図形は計算ミスが多くなる単元です。特にケアレスミスが多いお子様はより注意して取り組みましょう。
・情報の整理をしっかり出来る(式を乱雑にかかない)
・3.14の段を覚えている(計算が苦手なお子様ほど覚えましょう)
・3.14をまとめて計算している
基本になります。どれも確実に取れるようにしておきましょう。
A1の表面積は「上下・左右・前後・影」の4つに分けて整理して解くようにしましょう。また、「上下・左右・前後はそれぞれ面積が同じである」という発想ができているかも確認しましょう。
A2 B3 C3は円錐の3大公式(自称です)を覚えておきましょう。
・中心角=半径/母線×360° (ボブばーさん) ※中心角×母線=半径×360
・側面積=半径×母線×3.14 (図を参照)
・回転数=母線/半径 (半分の母さん)
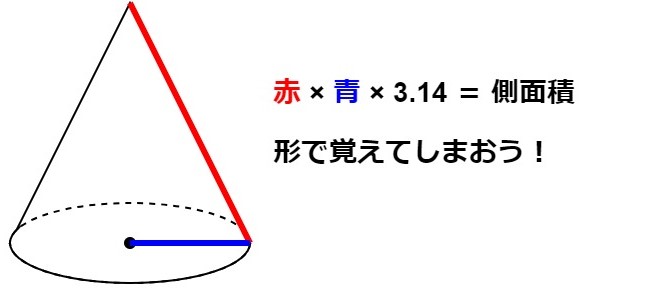
B3は中心角と半径の比の話です。結構使う考え方なのでしっかりと確認しましょう。
上記のひとつ目の公式を書き換えると「中心角:360=半径:母線」になります。暗記する必要はありません。なぜそうなるのか理屈で覚えてしまいましょう。
A3 C1は断頭〇〇柱です。平均の高さを取るという発想を持ちましょう。
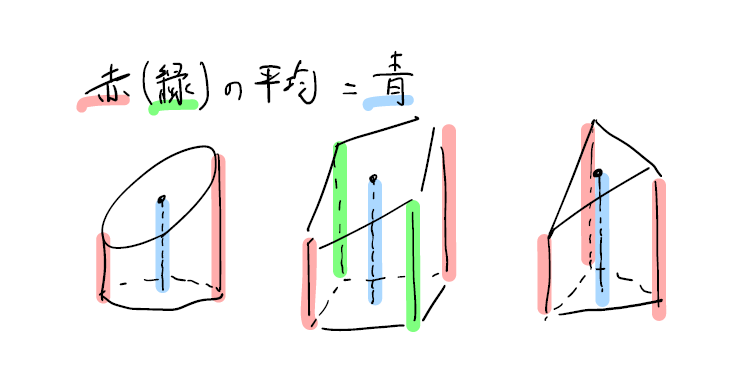
断頭〇〇柱は2020年と2022年のマンスリーテストで出題されています。
A4 B1 B2は展開図の問題です。
展開図から立体図形を組み立てられることと、どこの辺の長さがどこの辺の長さと同じなのか分かること。この2点を確認しましょう。
B1 B2では円が絡むので少し分かりにくい部分もあるかもしれません。B2では24㎝、25㎝というヒントからどこの長さに対応しているのかを分かっているか確認しましょう。
まずはしっかりと回転体の作図ができるかどうか確認しましょう。問題によっては作図は必要ありませんが、「かけるけどかかない」と「かけないからかかない」は天と地の差があります。
① 図形の角を線対称の位置にかく
② 半円で繋げる
以上の2つでかけます。
解くことに関してはどちらも複雑ではないですが、計算が合わなくなる可能性が高い問題なので、しっかりと情報を整理しながら解いているか確認しましょう。
また、どちらも3.14は最後に計算しているかも確認しましょう。分配法則を利用して最後にまとめて1回というのが原則です。
少し思考が必要です。しっかりと論理的に考えられているか確認しましょう。
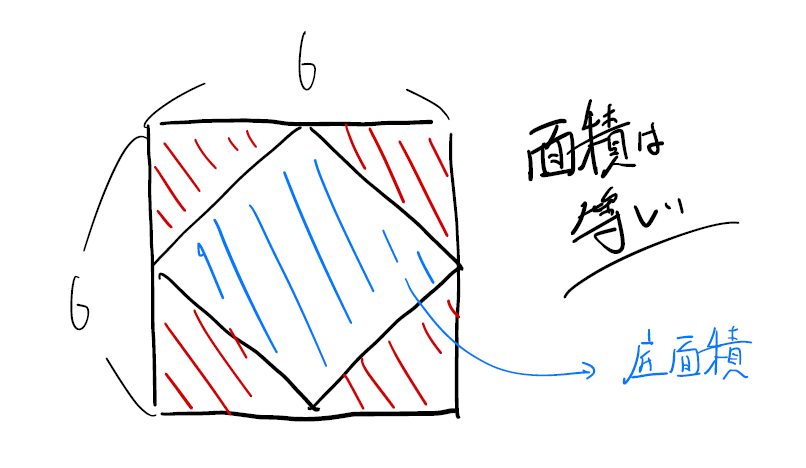
・容積を出すには「高さ」と「底面積」が必要
・「高さ」は正方形の一辺である → 64㎠の利用
・「底面積」は「179㎠−外側の面積(側面積)」 → 31㎝と「高さ」の利用
この思考が出来ているかどうかお子様に説明させてみるのが良いかと思います。
これは知識です。
覚えておきましょう。松田は折り紙などを使って説明しています。
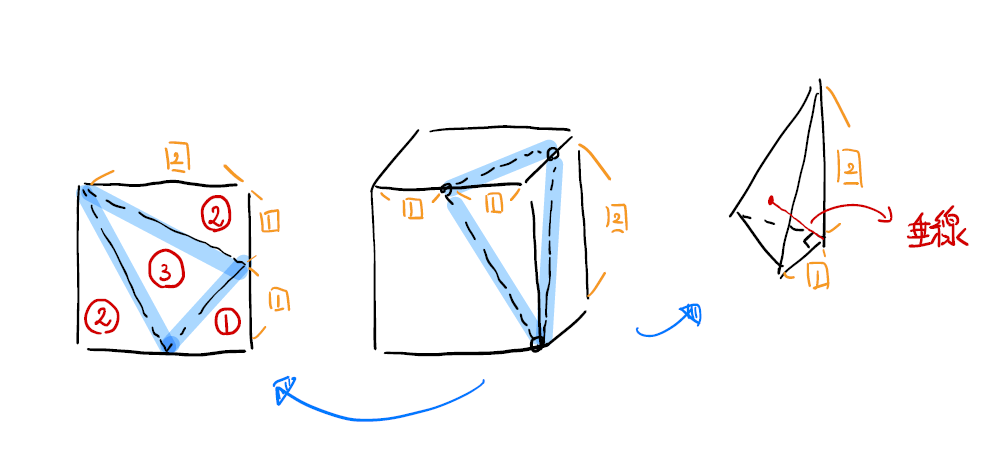
(2)の垂線を下す問題は「高さと底面積の変更」であると認識できているか確認しましょう。
この問題の類題が2020年と2022年のマンスリーテストで出題されています。
表面積の問題です。まずはA1と同じように「上下・左右・前後・影」と分けて情報を整理してかきましょう。また、しっかりと「上下・左右・前後はそれぞれ面積が同じである」という発想が出来ているかも改めて確認しましょう。
円錐の三大公式の「回転数=母線/半径」を利用します。まずはそれが思いついているか確認しましょう。
ただ、母線が途中で切断されているので、相似比を利用して母線を出しましょう。この相似の利用は基礎基本になるので、しっかり出来てほしいところです。
テキスト02のD3で出題された問題と同じ考え方です。1番遠い点と1番近い点をしっかり取れているか確認しましょう。
この三角錐の形はしっかりおさえておきましょう。断頭〇〇柱の発想を利用すると簡単です。三角形BCMを底面とし、高さの平均を取って計算しましょう。図形の中に底面積を置く発想はテキストH02のC4でも登場していますね。
E1やテキストH02のC4で登場した発想と同じです。底面を図形の中に置きます。この発想が出来ているか確認しましょう。
手順が多いですが、ひとつひとつは難しくないのでぜひ取り組みたいです。
まず「回転数」と「半径」から「母線」が求められているか確認しましょう。
次に、側面積ですが「母線×半径」を使います。そして、「全体−上部」で解きましょう。この全体から上部を引くという発想は様々な問題で登場します。しっかり身についているか確認が必要です。
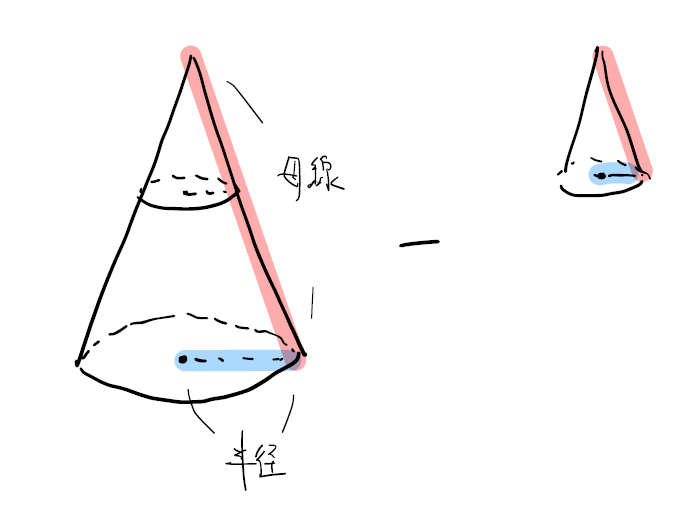
まずはしっかりどのような形になるのか想像できているか確認しましょう。お子様に作図をさせてみるのが良いと思います。
作図の方法は前述しているのでそちらをご参照ください。
形が想像できてしまえば後は難しくないです。
もちろんですが、3.14はまとめて計算しましょう。
また、体積比をすでに習っているお子様は体積比を利用して解いても良いかと思います。
大問形式で毎年のように出題され、また入試でも頻出の単元です。重要な単元ですので、しっかりやり込みたいです。
・グラフの意味が説明できる
・自分でグラフがかける
・相似の利用を意識できる
まずはしっかりとダイヤグラムから状況が読み取れているか確認しましょう。お子様に説明させるのが良いです。
速さを出して解いても良いですが、ここでは相似の利用が出来ているかを確認したいです。砂時計型(蝶々型など)とピラミッド型(A型など)を利用して、相似での解き方を確認しましょう。
まずはしっかりとグラフと水そうの関係を説明できるか確認しましょう。
(3)は体積を出さないで、「1分あたりの高さの変化量」を速さとし、その比から底面積の比を出して解く方法もあります。「1分あたりの高さの変化量」の逆比が「底面積の比」です。
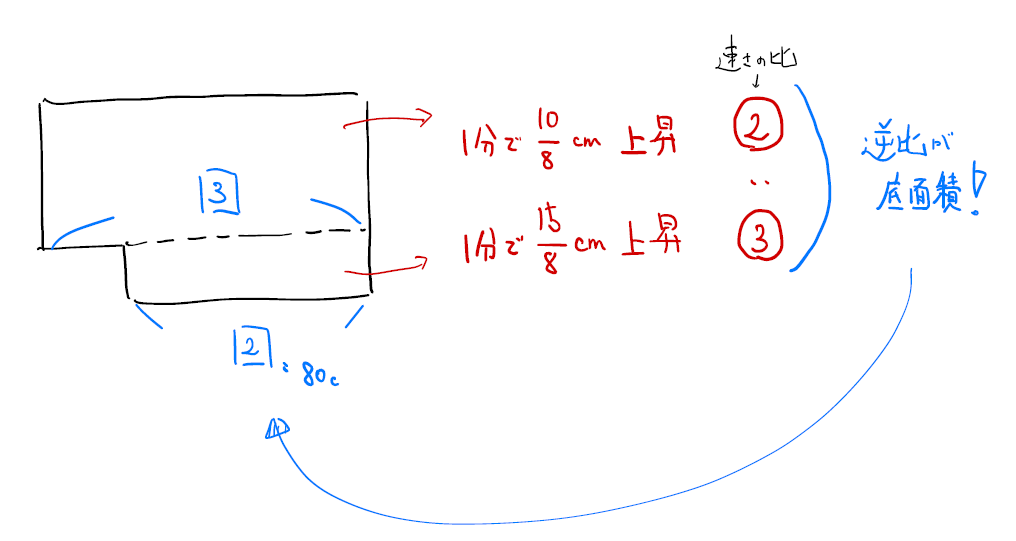
B1と同じ考え方をします。「1分あたりの高さの変化量」の逆比が「底面積の比」です。これを利用しましょう。
作図の問題です。
作図する機会はあまりないので、しっかりと作図できるか確認しましょう。
速さを出して解いても良いですが、こちらも相似を利用すると楽かと思います。C1とは違い、必要な情報が全て揃っていないので、自分で必要な情報を出す必要があります。
例えば(1)では、
・相似を利用すると方針が立てられている
・Aのろうそくを利用して必要な情報(1時間20分時点のろうそくの長さ)を出すという方針が立てられる
以上を確認すると良いかと思います。
速さの実数を(1)(3)で問われているので、基本は速さを出して普通に解いていくのが良いかと思います。ただし、(2)などは相似を利用すると一瞬で解けます。
(3)が出せるかどうかがひとつの壁かと思います。設問で使っていないヒントである「20分後」というヒントと、「前の問題を利用して次の問題を解く」という大問の特徴をおさえられているかが重要です。確認しましょう。
「図への書き込み」と「図から1メモリ5分であるという情報の読み取り」が出来ているかの確認をしましょう。これが出来ていれば(1)は容易です。「図への書き込み」は時速6kmというヒントと10:23に追い抜かれたというヒントしかないので、予測で大丈夫です。
(2)では「前の問題を利用して次の問題を解く」という発想をしっかり持てていれば難しくありません。確認しましょう。
しっかりと作図できるか確認しましょう。定規を利用しないでかくようにするとより実戦的な練習になるかと思います。
図がかけると2つの砂時計型の相似が登場します。差が50mというヒントから、2つの相似から得られた比を連比(比合わせ)を利用して差を取れば解けますね。この「差のヒント」→「比の差を取る」という動きは割合の単元でたびたび登場しているので、しっかりと確認しておきましょう。
間の関係を表したダイヤグラムです。入試では頻出なのでしっかりと練習しておきましょう。
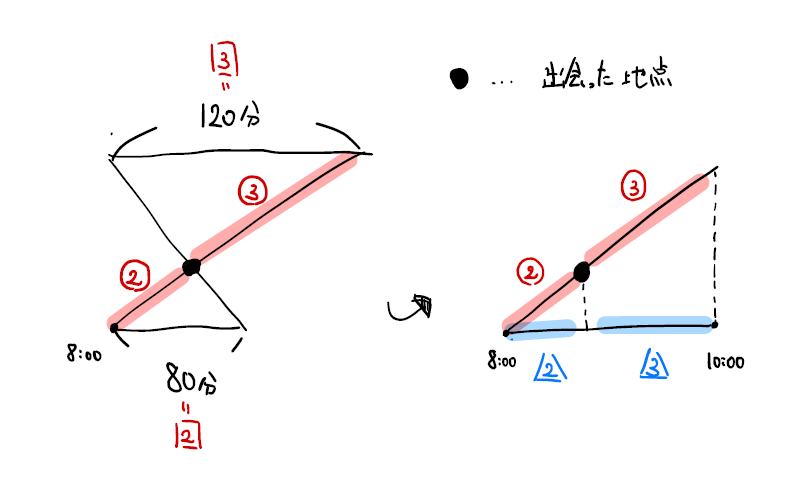
今回の問題ではしっかりとダイヤグラムの説明ができるかどうかを確認したいです。「この点が何を表しているのか?」「この線が何の速さを表しているのか?」をしっかり確認しましょう。元のダイヤグラムをお子様にかかせてみると良いと思います。
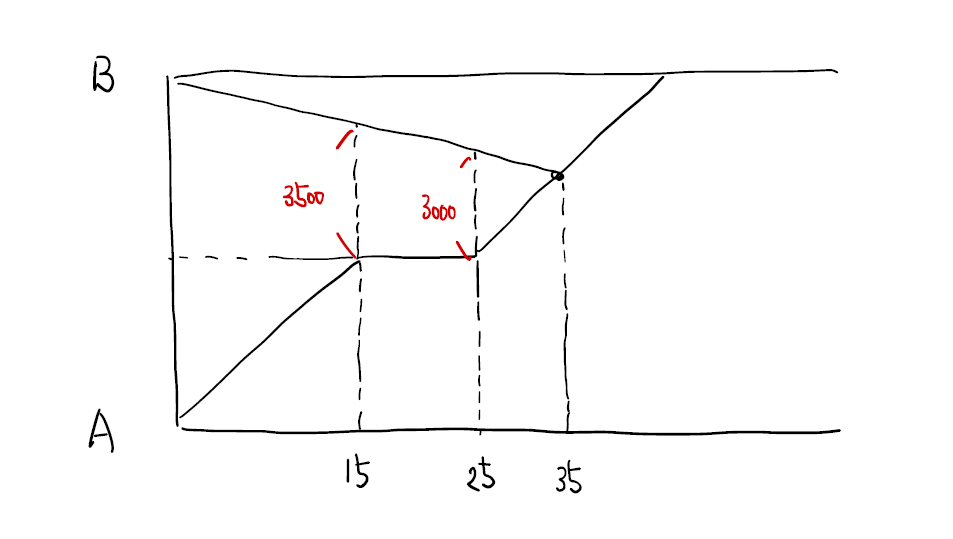
D3を発展させた問題です。
こちらも上記と同様にダイヤグラムの説明をさせ、確認すると良いと思います。
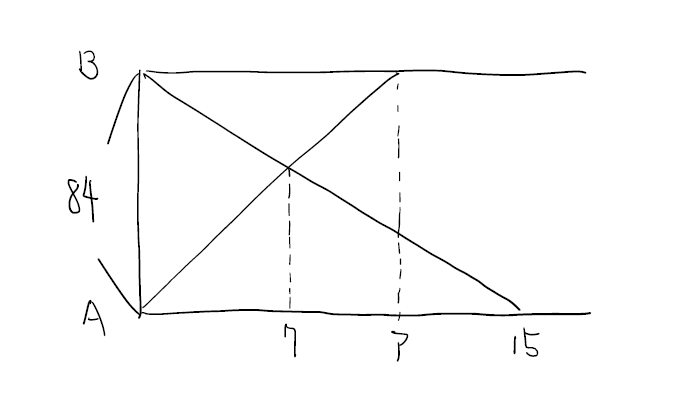
書いてある情報をしっかりと整理できるかが重要な問題です。
(1)は「6km C駅より」というヒントから和差算を利用すればすぐに解けますね。
(2)は「もし休まなかったら?」という発想をすると簡単です。この発想はよく使いますので、この機会にぜひ触れた方が良いかと思います。
(3)に関しては(1)と(2)の情報をまとめていけば大丈夫です。
毎年必ずと言って良いほど小問と大問で出題されます。特に大問ではパスカルの三角形の類題が非常に高い頻度で出題されていますので、規則性の発見方法をしっかりと学んでおきましょう。
・「同じ操作を繰り返す」→「規則性の発生」ということを理解している
・三角数、平方数(四角数)を覚えている、気がつける
・日暦算の基本を理解している
基本です。しっかりできるようにしましょう。B1の問題において、時々筆算をして全て計算しているお子様を見かけますが、1の位のみの計算で規則性は発見できます。念の為確認しておきましょう。
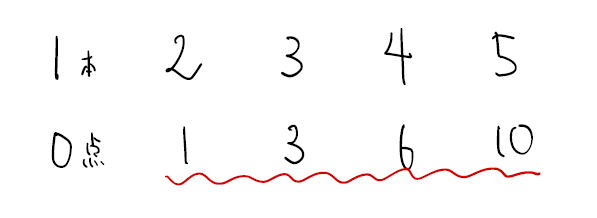
周りの個数と1辺の個数の関係を理解しているか確認しましょう。
「1辺の個数−1」=「周りの個数÷4」
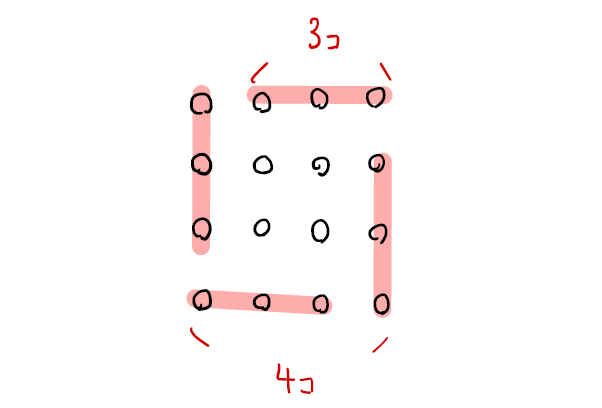
あとは全体の個数が「1辺の個数」×「1辺の個数」ということが分かっていれば解けますね。
規則性の発見方法がしっかりしているか確認しましょう。
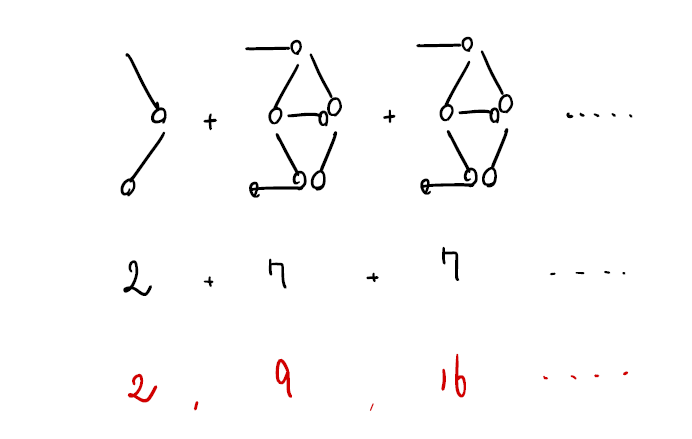
マッチ棒のような図形の規則性の問題は等差数列に置き換えて考えると分かりやすいです。今回の問題では「2で始まり、7ずつ増える等差数列」ですね。
日暦算の基本です。
「日数÷7」の余りを利用する、という基本ができているか確認しましょう。
また、今回の問題で翌年の4/4の曜日を先に出し、そこから戻るという解き方もできます。この解き方をする場合は、「翌年の同じ日の曜日が1つズレる」ということを理解しているか、またその理屈を説明できるかを確認しましょう。
規則性の発見の練習です。規則性をどうやったら見つけられるかをしっかり学びましょう。ポイントとしては、「表にまとめる」ということを松田は推奨しています。

奇数の和が平方数になることは知識としておさえておきましょう。平面図形の面積比の話などでも登場します。
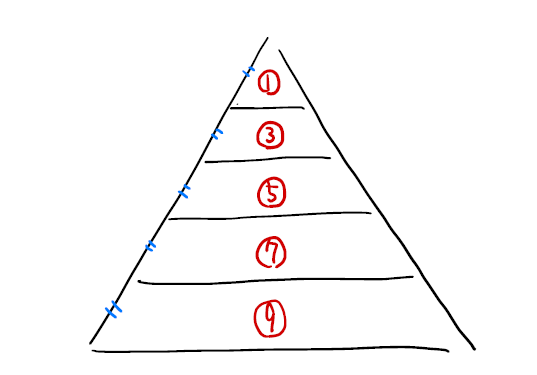
上記でも触れましたが、「翌年の同じ日の曜日が1つズレる」ということと「うるう年の場合は2つズレる」ことを理解しているか、またその理屈を説明できるかを確認しましょう。
注意が必要な点として、「うるう年だったとしても2/29にかかっていなければ2つズレない」という点です。
例えば、2024年の4/1は月曜日です。そして、2025年の4/1は火曜日です。1つのみのズレですね。2024年の2/29に触れていないためこうなります。注意しましょう。
パスカルの三角形です。
過去のマンスリーテストでも高確率で出題されている問題です。考え方をしっかりおさえておきましょう。
・規則性の発見(大抵の場合、三角数です)
・簡易的な図の作成
・追加の規則性の発見
以上をしっかりと意識していくと簡単です。
特に1つ目の「規則性の発見」が出来てしまえば芋づる式に解けることもありますので、しっかりと訓練しておきたいですね。コツとしては「お尻(端)に注目」です。
C1では格段の最後が三角数になっていますね。これを利用していきましょう。

(2)に関しても簡易的な図をかくと良いです。最後16段目を全てかいても良いと思いますが、間の数に注目すると簡単です。
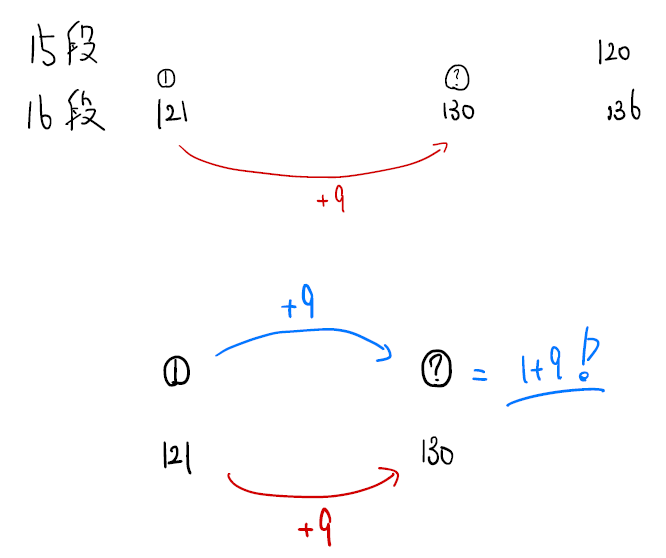
(3)は和の規則性を発見しましょう。
これもよく出る問題なので、おさえておきたいですね。段数ごとに和を出し、規則性を発見していくか、等差数列の和の公式を利用しましょう。しっかりと等差数列の和を出せているかは確認が必要ですね。
BとCの規則性を発見出来ているか確認しましょう。
意外と難しく、ついBを等差数列。Cを階差数列と考えてしまうお子様が多いかと思います。しかし、それだと問題を解くときに苦労しますので、注意が必要です。
ここでは「差を取る」以外の規則性の発見方法をしっかりと確認し、練習しておきたいです。
規則性を発見出来ているか確認しましょう。
方法としては前述しましたが、表にまとめるのがおすすめです。
規則性が三角数であることが分かれば後は簡単ですね。
これもC3と同様に規則性の発見が出来ているかを確認しましょう。
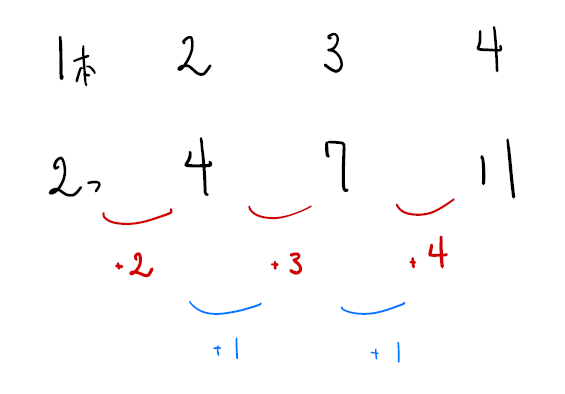
規則性が階差数列になっていますね。階差数列の計算がしっかり出来ているかも確認しましょう。
桁をばらしていく問題です。この種類の問題は3の倍数でないパターンもあります。
考え方ですが、丁寧に桁を分けて考えていきます。2桁の数は数列の2つ分になり、3桁の数は数列の3つ分になります。ですので、1桁の3の倍数と、2桁の3の倍数と、3桁の3の倍数を別々で考える必要があり、またこれらの数字を整理してまとめていく必要があります。
この発想がしっかり持てていることと、整理することが出来ているかの2点を確認しましょう。
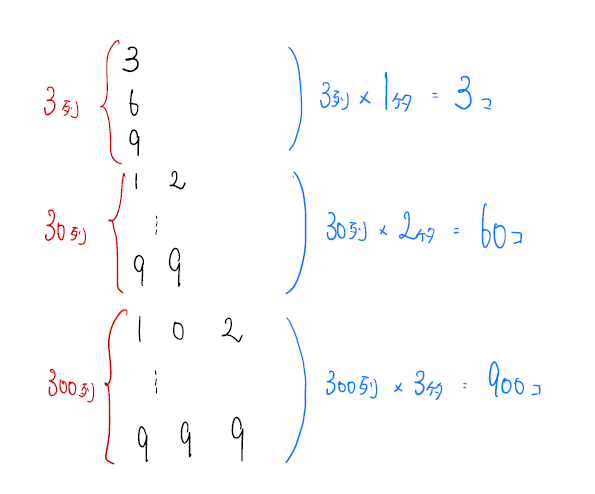
こちらもしっかりと規則性を取ることが重要です。図のようにまとめていくと分かりやすいと思います。
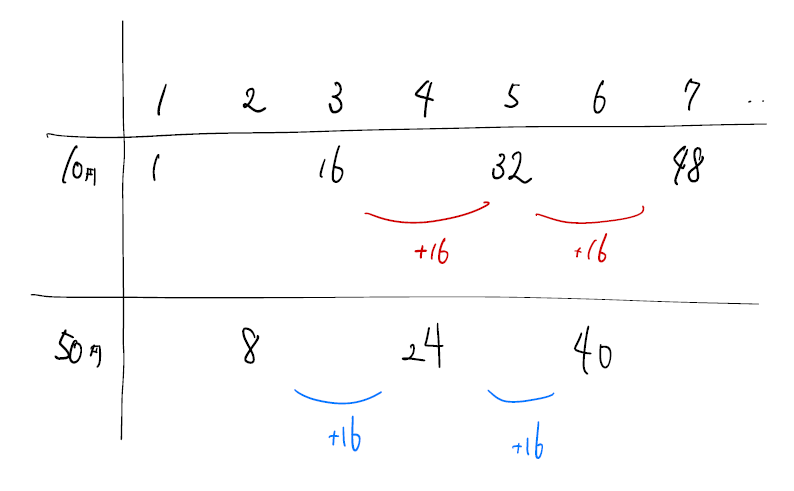
16ずつ増える等差数列になっていますね。後は解くだけです。
これも規則性を取りましょう。力ずくで規則性を発見する方法と綺麗に発見する方法があり、発想として両方とも知っておいて損はないので、確認しましょう。
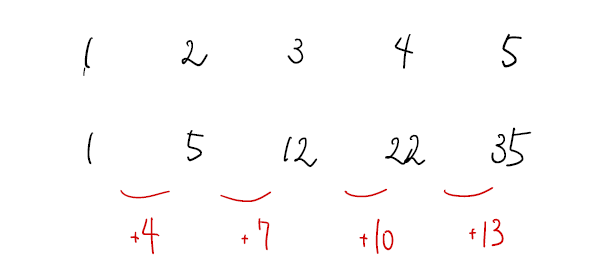
規則性の発見と「●○◎」の周期を利用するということに気がつけているかを確認しましょう。
パスカルの三角形の類題です。マンスリーテストでもよく出題されているので、必ず確認したいところです。
規則性の発見が出来ているかをしっかり確認しましょう。
(1)はかいていけば解けますね。ただし、かくと言っても全てかいていくのではなく、部分的に必要な情報だけかきましょう。この部分的にかくという解き方は使えますので、覚えておきましょう。
(2)は規則性を発見できれば容易です。
1,2,4,8,16…となっていることに気がつければ後は簡単ですね。
マンスリーテストではそこまで多く出題されていませんが、カードの問題や硬貨の問題はよく出題されています。まずは頻出分野をおさえておきましょう。
・+と×の判断が正確にできる
・順列と組み合わせの違いが説明できる
・場合分けができる
・整理して調べ上げができる

ちなみに松田は「場合分けをする時は足し算」「それ以外は掛け算」と教えています。正確には「可能性が同時に存在する場合が掛け算」「可能性が同時に存在しない場合は足し算」となるのですが、これだと生徒が理解してくれないので、上記のように伝えています。
基本的な問題です。しっかり解けるようにしましょう。
A1では
・3の倍数
・4の倍数
・5の倍数
の見分け方は最低限知識としておさえておきましょう。
余裕があるお子様は
・6の倍数
・8の倍数
・9の倍数
まで覚えておきましょう。
また、カードの問題では同じものを数えないように、「大きい順or小さい順」で調べるという癖がしっかりついているか確認しましょう。カードの問題はマンスリーテストでは頻出なのでしっかり出来るようにしたいです。
硬貨の問題です。この3つバージョンがマンスリーテストでは頻出です。
不定方程式(芋づる算)の考え方を利用します。しっかりとまとめて調べられているかを確認しましょう。
碁盤の目になっている道順の問題です。マンスリーテストでもちょこちょこと出題されています。
数字をかき入れて数えるパターンと計算するパターンがあります。まずは普通に数えるパターンで解けるようにしましょう。意外と数え間違えるお子様は多いので、見直しをする癖をつけましょう。偏差値50以上を狙っていく場合は、両方とも出来るようにしたいですね。
まず、この問題が組み合わせであるということに気がつけているか確認しましょう。「選ぶ」という発想をする時は「組み合わせ」になると覚えておいても良いでしょう。
組み合わせと気がつければ後は簡単ですね。
仕組みは最悪分かっていなくても良いと思っています。もちろん分かっている方が良いのですし、上位を狙っていく方は分からないとダメですが、そうでないお子様の場合、仕組みよりも解けることを優先した方が良いです。
場合分けの発想が出来ているか確認しましょう。
・3種類使う場合
・2種類使う場合
・1種類使う場合
場合分けは使える考え方です。「困ったときの場合分け」と覚えておくと良いでしょう。
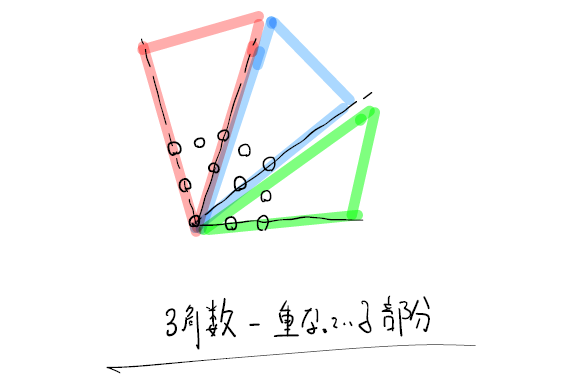
この発想を身につけておきましょう。道順と同じ考え方です。考え方さえおさえてしまえば簡単です。
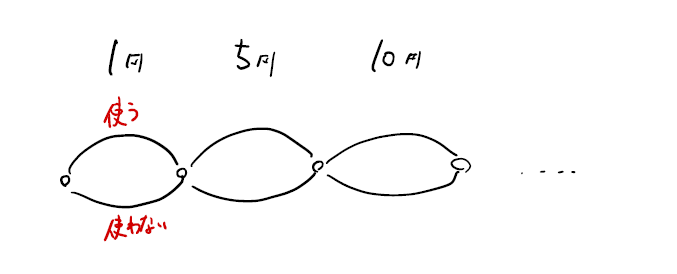
適当に調べていないかどうか確認しましょう。抜け漏れがないように調べられていれば問題ないです。
使用する考え方は碁盤の目の問題と同じなので、その考え方に辿り着けるかどうかです。
(1)は樹形図でしっかり調べあげましょう。調べあげる時の最終手段は樹形図です。
(2)は先頭に3を使った場合、「3,1,○,1,○,1」という形しかないということに(1)を解いている最中に気がつけるかが大事です。まずは「3,1,○,1,○,1」という形しかないということに気がついているか確認しましょう。
(3)では「1が先頭の場合」と「3が先頭の場合」を(1)(2)で出しているので、「2が先頭の場合」を求めれば全て調べ切れる、ということに気がついているか確認しましょう。
発想として重要なので身につけておきたい問題です。
まず合計が15なので、3枚の和が9or11の奇数である、ということに気がつけているかどうか。そして、3枚の和を調べるのではなく、残った2枚の和が6or4であり、この通り数を調べるという余事象の発想が出来ているかどうか。この2点を確認しましょう。
和分解の考え方を使います。間違っても数えていかないように注意しましょう。
(1)は二等辺三角形なので、(1,1,6)(2,2,4)(3,3,2)の3つの種類があることが分かります。この発想が出来ているか確認しましょう。
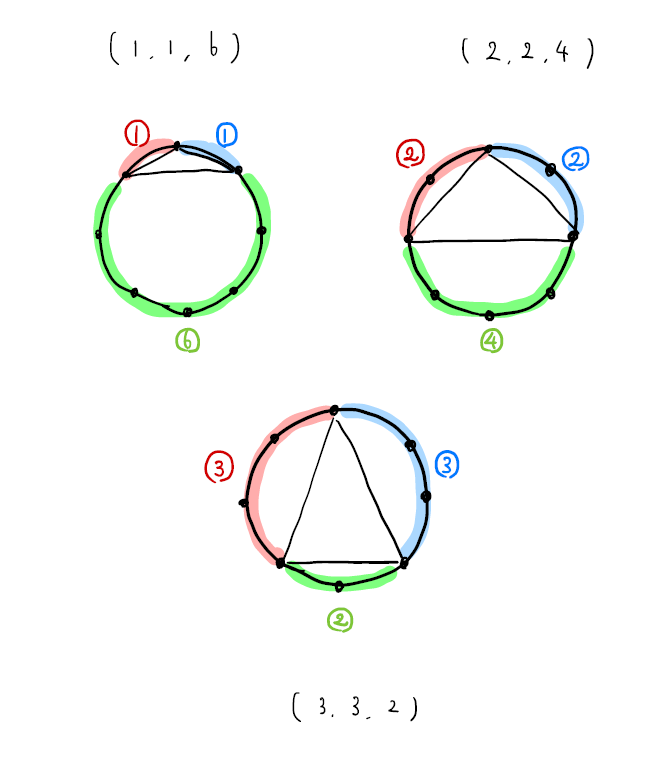
E3では同じ発想でしたが、「回転したり、裏返したり重なるものは同じ」という文言から(1,1,5)と(1,5,1)、(5,1,1)はいずれも同じと考えます。
(2)は直角三角形のパターンです。ここで「直径を通ると直角三角形になる」という知識を確認しておきましょう。直径を通るので(4,○,○)となり、4を固定して考えましょう。
順列と組み合わせを利用した問題です。計算で出します。間違っても数えないように注意しましょう。
直線ℓの4点から2点を選ぶ。直線mの5点から2点選ぶ。「選ぶ」なのでそれぞれ「組み合わせ」です。
そして、直線ℓが6通りで直線mが10通り。場合分けをしていないので掛け算をする順列で計算をしましょう。
調べ上げの問題です。丁寧に調べていきましょう。
解説は以上となります。
少しでもご参考になればと思います。
SAPIX新6年4月マンスリーの各教科の解説はこちらをご覧ください!
SAPIX新6年4月マンスリーで押さえるべきポイント!算数編
SAPIX新6年4月マンスリーで押さえるべきポイント!国語編
SAPIX新6年4月マンスリーで押さえるべきポイント!理科編
SAPIX新6年4月マンスリーで押さえるべきポイント!社会編
にほんブログ村にも参加しています。ぜひ下のバナーをワンクリックで応援もお願いします!
![]()
この記事を書いたのは...
松田 浩志
自律学習サカセルでは算数・国語、主要2科目を担当。
大手進学塾では、教務主任職として、校舎全体の運営を担当し、日曜日の志望校別コースの最上位クラスから自校舎の基本クラスまで、算数・国語の両科目で毎年幅広くクラスを担当してきた。
現在の趣味はファッション。
もともと古着が好きだったのですが、現在は「キレイめ」なファッションが好み。