芝中の算数分析（2018年 第1回）

東京タワーの真下、都心の真ん中に位置する芝中学。

伝統ある進学校で多数の有力なOBを輩出してきました。

温かく、生徒の自主性を尊重する校風も人気で、多くの受験生を集めます。

中学受験においては、国語・社会における記述式の問題が大きな特徴として挙げられます。

算数は50分で大問10問弱、答えのみが問われる形式。

受験者平均と合格者平均では例年15点前後の差がつき、算数で合否が決まるとも言えそうです。

特に差がつく分野は「平面図形」と「速さとグラフ」が挙げられます。

この2分野は過去問を通し、頻出テーマを深く理解しておく必要が高いです。

ここからは2018年第1回の算数の入試問題を通して、どうすれば芝中学に合格出来るのかを考えてみましょう。

〇：芝中学合格のために確実に正解したい問題

△：合否を分けた問題

□：正解できなくても合否には影響しない問題

大問1

(1)　○

芝中らしい、やや繁雑な計算問題です。

丁寧に処理していきましょう。

(2)　○

こちらも芝中らしい面倒な計算問題です。

丁寧な逆算が求められます。

なお芝中の計算問題は、途中経過は汚い数値が出ることも多いですが、最終的な答えは比較的きれいな数になることが多いことも特徴として挙げられます。

大問2　○

単純な計算問題です。

全て足して10で割っても良いですし、仮平均を15gとして、それより何g多いかを計算しても良いでしょう。

ここまでの3問は、たしかに計算量は多いものの、決して難しくはないので全問正解しておきたいところです。

大問3　△

食塩水のやり取りの典型題です。

「最終的には5％の食塩水300gのAと□％の食塩水100gのBを混ぜると、5.5％の食塩水400gが出来た」というように、後ろから考えることがポイントです。

方針さえ立てられれば、あとは面積図でも天秤でも、自分の得意な方法で丁寧に処理しましょう。

大問4　△

「何が変わらないかに注目する」というルールに則って、線分図で整理して考えましょう。

今回は差が変わらないので、Cの残金を①とすると、Bの残金は②－200、Aの残金は⑥＋100となり、このAとCの差が2600円と分かります。

大問5

(1)　○

「0がいくつ並ぶ？」⇒「×10がいくつ？」⇒「×2×5が何組？」⇒「素因数分解して5が何個？」と言い換える、中学受験における典型題です。

今回は範囲が途中からですが、20で1個、25で2個、30で1個と丁寧に調べましょう。

(2)　×

「4で何回割れる」＝「(2×2)を何組？」と言い換えましょう。

2006から2018までの偶数を素因数分解したときに2が何個出てくるかを数えるだけですが、時間がかかるので後回しにしても良いでしょう。

大問6　○

芝中において難問が課されることの多い、中盤の平面図形と比ですが、この問題は易しいでしょう。

1辺1cmの正三角形の面積を①とした時に、各箇所の面積がどうなるかを考えましょう。

大問7

(1)　○

芝中の速さはグラフや比を活用する難問で知られますが、この問題は易しいです。

速さがテーマではあるものの、実質は「20km/時と80km/時で、あわせて5.1時間で300km進む」という、つるかめ算です。

確実に正解しましょう。

(2)　○

(1)より、264kmの高速道路を3時間18分で進む予定だったことが分かります。

これよりも18分、所要時間を短くするだけなので易しいでしょう。

(3)　○

「80km/時と60km/時で、あわせて3時間32分で264km進む」という(1)と同じ発想で考えるつるかめ算です。

後半の大問としては非常に易しいので、やや繁雑だった前半でも焦らずに適切な時間配分が出来た受験生にとっては得点源となったことでしょう。

大問8

(1)　○

1～12までの2段を1セットと考えましょう。

500÷12＝41セット・・・8

41セットで82段と、あとは8がどこにあるかを考えたら大丈夫でしょう。

(2)　×

(1)と同様に2段を1セットと考えましょう。

1セット目の和は12、2セット目の和は36、3セット目の和は60…という等差数列になります。

あとは11セット目～25セット目の和を求めて、それから51行目の5列目の数を求めます。

処理量が多い問題なので、後回しにすることも有効でしょう。

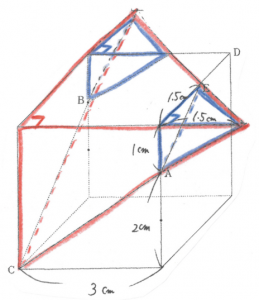
大問9　△　△

男子難関校頻出テーマの「立体の切断」です。

今回は以下のように「同一平面」⇒「平行」⇒「延長」のセオリー通りに取り組める典型題なので、比較的取り組みやすいと言えるのではないでしょうか。

体積を求める際は赤の三角錐と青の三角錐の体積比が3×3×3：1×1×1になることを利用しましょう。

なお求める部分は点Dを含む立体なので、全体から引くことも忘れないよう気を付けましょう。

2018年の芝中の第1回の算数は、受験者平均点が55.1点、合格者平均点が71.1点と、やや取り組みやすい出題となりました。

全15問の内訳も〇が9問、△が4問、×が2問と、得点すべきものが明確です。

合格のためには〇で8/9、△で2/4、×で0/2の10/15＝約67点が目安となりそうです。

大問5(2)や大問8(2)など、時間のかかる問題を後回しにすることで、合格ラインに到達する可能性はかなり高められたのではないでしょうか。

来年以降、芝中への合格を目指す皆さんは、第2回の問題や、もう少し難しい年度にも積極的にチャレンジしておきましょう。

平面図形と比における相似の使い方や対称性の利用、速さと比におけるグラフの利用など、芝中で頻出の難関テーマを克服することで、合格はより近づきます。