渋谷教育学園幕張中の算数分析（2019年 1次）

受験者平均点　39.4点

合格者平均点　53.2点

想定合格点　　50点

渋谷教育学園幕張中学校の学校の特徴や傾向分析、2018年第1回の分析はこちら

2019年1月22日、渋谷教育学園幕張中学校の入学試験が実施されました。

例年よりやや少なかったとは言え、今年度も2000名を超える受験生を集める激戦。

見事に合格を勝ち取った皆さん、おめでとうございます。

ただ多くの受験生は、まだまだ入試が続きます。

結果は結果と受け止めて、次の試験に向けて準備を進めましょう。

ここからは、

〇：渋谷教育学園幕張合格のために確実に正解しておきたい問題

△：出来不出来の差がつきやすい問題

×：出来なくても差がつかない難問

として今年度の出題を見ていきます。

今年度の出題において合格を勝ち取るためには、どこで得点すべきだったのかを確認していきましょう。

大問1

(1)　△

題意の確認問題ですが、第1問としては、やや時間がかかります。

Aの14□□は6通りなので、16□□も6通り、17□□も6通り、ここまでで18通りなので、1946、1947と調べましょう。

BはAのカードとの対応関係を考えて2938となります。

(2)　△

千の位に注目すると、(A,B)=(1□□□,2□□□)と(7□□□,8□□□)のときが、それぞれ4×3×2＝24通りの、ここまで合わせて48通り。

AとBの千の位がどちらも9の時は百の位まで注目して、(A,B)=(91□□,92□□)と(97□□,98□□)の、3×2×2＝12通りとなります

場合分けがやや面倒ではあるものの、ここまでは正解したいところです。

(3)　△

まずは千の位に注目すると、Aが6でBが4の時に差が最大になることが分かります。

次にAの百の位以下を大きく、Bの百の位以下を小さくすることを考えると、64□□と43□□となります。

あとは十の位が9になることに気づいて丁寧に調べていくと、(A,B)=(6491,4392)と(6497,4398)と分かります。

大問2

(1)　〇

非常に基本的な３進法です。

1の位、3の位、9の位、27の位と順番に考えていきましょう。

(2)　〇

(1)と同様、確実に正解したい問題です。

27×1+9×2+3×0+1×1と処理しましょう。

(3)　〇

(3)まで基本問題が並びました。

2019÷729＝2・・・561

561÷243＝2・・・75

75÷81＝0・・・75

75÷27＝2・・・21

21÷9＝2・・・3

3÷3＝1・・・０

なので、三角形を9マス塗ると考えましょう。

この大問は数分で完答したいところでした。

大問3

(1)　〇

題意の確認問題です。

Kには2:27に着いて2:32に乗るので待ち時間は5分

Mには2:29に着いて2:30に乗るので待ち時間は1分

となることを確認しましょう。

(2)①　×

以下のように、表を作って丁寧に調べましょう。

5分と8分が周期なので40分後までを考えます。

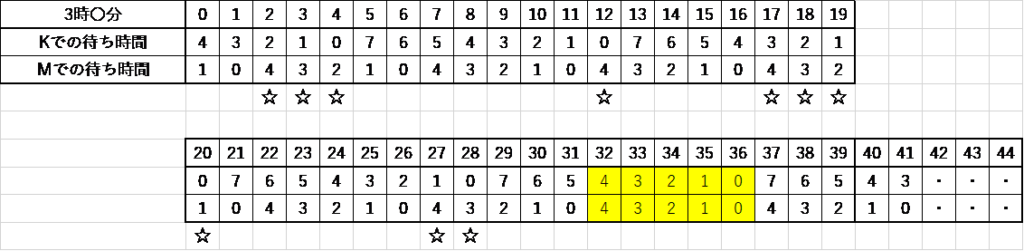
32～36で同じ数値が出てきますが、Mは31分を過ぎた瞬間からKと待ち時間が等しくなることに気を付けましょう。

処理量が多く、言葉の意味も取りにくい、得点効率の良くない問題です。

(2)②　×

①の表で考えます。

☆の箇所がKでの待ち時間が少ない箇所なので、丁寧に調べましょう。

大問4

(1)①　△

同じ角度に同じ記号をふって相似を探します。

ただ今回は以下のようにCからADに垂線を引かないと難しいかもしれません。

なお三平方の定理を使えるならば、使ってしまってもかまいません。

(1)②　△

今度は以下のようにGからCEに垂線を引くと良いでしょう。

△EDGと△EABが相似になることを利用します。

①②いずれも発想系の問題なので、解法が浮かばなければ後回しにしてしまって構いません。

(2)　△

ｘｙそれぞれの角度は求まらないが、和なら求まるという類題を経験し、思い出せるかが勝負です。

以下のように方眼を考えると解きやすいでしょう。

補助線を引くことで直角二等辺三角形が見えてきます。

こちらも発想勝負の問題なので、解法が浮かばなければ後回しにするべきでしょう。

大問5

(1)　△

切り口自体は難しくないものの、その後の計算量がやや多い問題です。

まずは以下のように上に延長して、四角錘台と捉えましょう。

高さは与えられていないので、計算しやすいよう3cmと設定してしまって構いません。

三角錐台の体積は

12×9×3÷3の三角錐を(2×2×2)：(3×3×3－2×2×2)の8：19に分けた19なので76㎤と分かります。

Aを含む体積は底面が8×1÷2で高さが6・6・9の断頭三角柱の28㎤になるので、あとは計算するだけですね。

難問ですが立体図形の演習を充分に積んでいれば、正解することも可能です。

(2)①　△

以下の図のように「向かい合う平行な面の切り口は平行」を利用すると、PQと平行になるようにFから補助線をHEの延長線と交わるまで伸ばしましょう。

捉えにくい問題ですが、正解することも可能でしょう。

(2)②　×

Aを含む立体を平面をABPQとする四角錘と、残りの三角錐に分けて考えると良いでしょう。

非常に難度が高いので試験時間中に解く必要は無いでしょう。

このように2019年第1回の渋谷幕張中の出題は、大問2だけが異常に易しく、残りは解きにくい問題が並びました。

小問ごとの難度を集計すると〇が4問、△が8問、×が3問で計15問。

合格のためには〇で4/4は必須、△で4/8を取って、なんとか8/15をかき集めたいところでしょう。

大問1と3の作業の精度がポイントと言えるのではないでしょうか。 

ただ今回の内容は

①　大問2が極端に易しいこと

②　大問3の問題文の意味の捉えにくいこと(丁度駅に着いたらどうする、間をどう捉える等、問題の本質以外での注意点が多い)

③　大問4の過度に発想に偏った問題、(1)は数学の知識で解けてしまうことも中学受験の算数の出題としては不適切では

④　大問5の立体の難度の高さ(立体図形が数多く課される男子難関校志望生は取り組んでいても、女子難関校志望生はあまり取り組んでいない)

など、生徒の学力を正確に測ることが出来るのか、という点で、僕にとっては多少の疑問が残る出題でした。

来年以降、渋谷幕張の合格を目指す皆さんには、とにかく「取れるものを確実に取る！」

そんな判断力と正確さを磨きましょう、としか言えません。