慶應中等部の算数分析（2018年）

慶應義塾大学三田キャンパスに隣接する、慶應義塾中等部。

自由な校風の男女共学校で、しかも慶應義塾の附属校ということもあり首都圏屈指の人気校として知られています。

そのぶん入学難度も非常に高く、特に女子の募集人数は約50名という狭き門。

知識の量とスピードが問われる1次試験と、慶應らしさの問われる2次試験。

合格基準が明確にされていない点、講師としては明確な対策が取りにくいことは否めませんが、1次試験での高得点が合格に直結することは確実です。

なお算数の解答用紙の記入形式は独特なので、過去問演習の際も必ず解答用紙に記入することで慣れておきましょう。

ここからは2018年の出題を通して、慶應義塾中等部の算数で合格ラインを越えるための方法を考えてみましょう。

○：慶應義塾中等部合格のために確実に正解したい問題

△：合否を分ける問題

×：正解できなくても合否には影響しない問題

 解答例はこちら

大問1

(1)　△

様々な工夫を詰め込んだ計算問題です。

分数⇔小数の変換や、3.5でまとめる工夫は定番ですが、70.2×69.8＝70×70－0.2×0.2と置き換える工夫は知らない受験生も多いことでしょう。

(2)　○

やや面倒な逆算です。

1.875＝1と7/8と置き換え、丁寧に計算していきましょう。

(3)　○

基本的な食塩水の問題です。

天秤か面積図で適切に整理しましょう。

(4)　○

最初の日曜日が1/7日なので、その22週間後＝154日後と考えましょう。

日暦算はやや計算量が多いものの、発想は難しくないので確実に正解したい分野です。

大問2

(1)　○

連比の基本問題です。

比の学習の導入レベルの出題なので確実に正解しておきましょう。

(2)　○

損益算の基本問題です。

□×1.3×0.8＝□×1.04なので、原価の0.04倍が34円にあたると捉えましょう。

(3)　○

旅人算の基本問題です。

初めて追いつく＝1周差がつくと言い換えましょう。

(4)　○

はじめの金額を(4)と設定すると考えやすいでしょう。

兄は(1)＋(1.8)－100円、弟は(1.2)＋100円＝700円と設定できます。

大問3

(1)　○

折り返しの基本問題です。

「折り返す前後が同じ」「錯角の利用」を心がけましょう。

アを⑧、イを⑤とすると、結局90度＋(⑧＋⑤)＋⑤＝180度と考えられます。

(2)　○

イ：エ＝3：1より、ア：ウ＝３：１で、ウ＝24㎠となります。

またウ：エ＝2：1より、エ＝12㎠と分かります。

結果、正方形の面積が144㎠と分かるので、1辺が求まります。

(3)　△

図のようにどの辺とどの辺が対応するかを考えてみましょう。

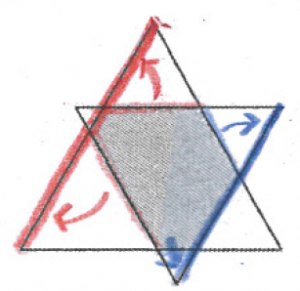
結局、大きな正三角形の1辺と、小さな正三角形の1辺の和と言い換えることが出来ます。

(4)　△

円柱と円錐台の組み合わせで、難度は高くはないものの、計算量の多い問題です。

スピードに不安がある場合は後回しにしても良いでしょう。

大問4

(1)　○

太郎は時速4km、次郎は時速16kmと求めて旅人算として解いても良いでしょう。

ただ以下のようにダイヤグラムの相似を利用できると、より早く正確に正答が求められそうです。

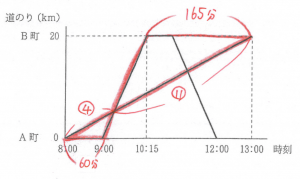
(2)　○

(1)と同様、以下のようにダイヤグラムと相似を利用しましょう。

難関校志望者なら確実に使いこなしたい解法です。

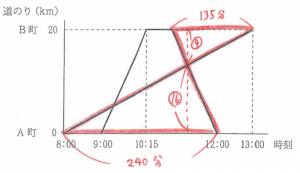
大問5

(1)　△

Aを□□奇、Bを□□偶と置いてみましょう。

Aの1の位は奇数だから5通り、Bの1の位は偶数だから4通り。

残ったカードは自由に置くことが出来るので、(7×6×5)×(5×4×4)と考えることが可能です。

(2)　△

差が最小の時は5□□(小)と4□□(大)の時なので512と498、

差が最大の時は9□□(大)と1□□(小)の時なので987と123となります。

(1)より取り組みやすいのではないでしょうか。

大問6

(1)　○

Aは75秒周期、Bは100秒周期なので、最小公倍数の300秒＝5分を1つの周期だと考えましょう。

(2)　△

以下の図のように整理すると考えやすいでしょう。

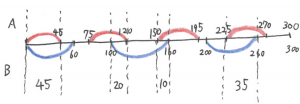
結局300秒のうち110秒なので

84÷5＝16周期…4分、この4分には90秒含まれるので、

110秒×16回＋90秒と考えることが出来ました。

大問7

(1)　○

正三角形を作るために必要な枚数は1、4、9、16、25…と平方数になります。

そこから140以下の最大の平方数は11×11＝121枚と考えてみましょう。

(2)　×

(1)より正三角形を作るために必要な枚数は平方数、また正六角形は正三角形を6つ集めたものであることに注目すると、

平方数＋平方数×6のうち140に近い最大の組み合わせと分かります。

平方数は、1、4、9、16、25、36、49、64、81、100…

平方数×6は、6、24、54、96…

ここから答えに該当する組み合わせを探しましょう。

今年も例年通りの全20問となりました。

○が13問、△が6問、×が1問という内訳なので、

男子なら、○で12/13、△で3/6で、×0/1で合計75点、

女子なら、○で12/13、△で4/6で、×0/1で合計80点あれば、1次試験を算数が原因で失敗することは無いでしょう。

また2次試験でリードをとるためには、男女ともにあと1問ずつ取れれば充分でしょう。

本番の緊張下の試験、巷で言われるような「９割必要！」ということはさすがにありません。

来年以降、慶應義塾中等部合格を目指す皆さんは、まずは中学受験算数の基本パターンの問題を早く正確に解ける学力の養成を目指しましょう。

その上で過去問演習を通し、時間がかかる問題や、難度のやや高い問題の「捨て方」を身につければ、合格のチャンスは拡大しますよ。