想定合格点 55点
女子学院中学校の学校の特徴や傾向分析、2018年の分析はこちら
女子学院の算数は例年、40分の制限時間で20~30問の標準レベルの問題が課されます。
ここ数年は難度は特に抑えめで、合格のためには80点以上を目安にしたいところでした。
ところが2019年は状況が一変しました。
出題量はあまり変わらないものの、個々の問題の難度が大幅に上がり、算数の合格ラインは大きく下がったと想定されます。
ただ出題傾向が変わっても、女子学院の合格者のレベルは変わりません。
ここからは2019年の出題において、どこを正解すれば合格に近づくことが出来たのかを、個々の問題を通して見ていきましょう。
〇:女子学院合格のため必ず正解したい問題
△:合否の分かれ目になる問題
×:間違えても合否には影響しない問題
大問1
(1) 〇
標準的な計算問題です。
673×3=2019なので、年号にちなんだ数値設定でした。
(2) 〇
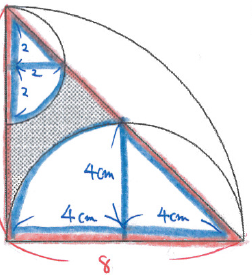
基本的な面積の問題です。
「おうぎ形は中心と境目に注目」という鉄則から補助線を引きましょう。
すると下の図のように、直角を挟む2辺が8cmの直角三角形から、直角を挟む2辺が2cmの直角三角形と、直角を挟む2辺が4cmの直角三角形、半径2cmで中心角90度のおうぎ形と半径4cmで中心角90度のおうぎ形を引けばよいと分かります。
(3) 〇 〇
標準的な約束記号の問題です。
①では1-[A]=1/3
[A]=2/3
A=3/2
のように処理しましょう。
②も同じように処理することが可能です。
ここまでは決して難しくはないので、無失点に抑えたいところでした。
(4) △ △ △
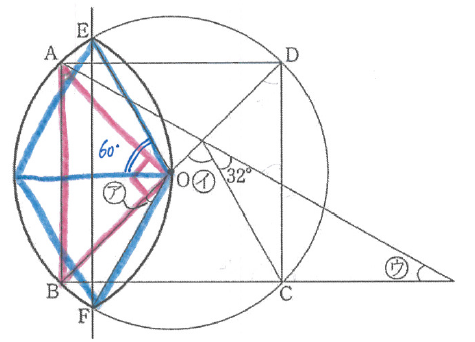
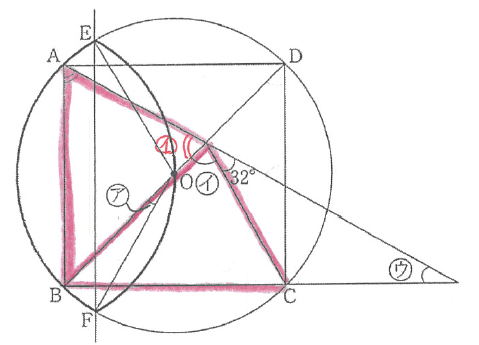
円の特徴や折り返しの特徴を利用した角度の問題で、なかなか気づきにくいぶん難度は高めです。
アは以下のように正三角形と直角二等辺三角形に気づけるかがポイントです。
イとウは、以下のように合同な三角形に気づけるかがポイントでした。
(5) △ △
青+白>赤の場合と、青+白<赤の場合に分けて考えます。
赤=①+5
白=①
青=シカク1
とおいて処理しますが、この文字式の処理が苦手な受験生も多いことでしょう。
大問2
(1) △
左から5cmの直線、直径2cmで中心角90度のおうぎ形、直径6cmで中心角120度のおうぎ形、直径2cmで中心角60度のおうぎ形、5cmの直線になります。
面倒ではあるものの、発想は定番なので正解しておきたい問題です。
(2) △
「回転数=中心が動いた距離÷円周」のルールに沿って解けば、ちょうど1周した時だと分かります。
理屈を正しく理解し、問題に応じて使い分けることは難しいので、解法知識として知っておきたい内容です。
大問3
(1) ×
立方体の展開図は11種類ありますが、12を含むものを丁寧に調べ上げる時間の余裕はないでしょう。
後回しにしても問題ありません。
(2) △
出来る限り小さな数を多く選ぶようにしたい問題ですが、出てきた答えに確証を得ることは難しいでしょう。
「とりあえず見つかった小さそうなもの」を解答として記入すれば充分です。
大問4 △ △
56と4/11分で310度、長針は短針より多く進むので、この時点では短針が長針より130度前にいることが分かります。以下の図のように考えると、●時ちょうどよりも短針は10度進んでいるので、10÷0.5=20分と分かります。
初見なら難しいものの、様々なテキストで類題が掲載されているので、女子学院合格のためには正解したいところでした。
大問5 △ △
全部の個数は「12の倍数+6個」かつ「15の倍数+9個」となり、いずれも「6個足りない」ことから「60の倍数-6個」と言い換えることが出来ます。
54個の場合は600円の差、114個の場合は900円の差、174個の場合は1200円の差・・・と等差数列になることを利用して答えを導きましょう。
売り上げを最大にする時は、単価の高い12個入りを多くする場合から考えます。
最大で69箱用意できますが、この時は6個余ってしまいます。
68箱、67箱・・・と減らしていって、最も無駄がない場合を考えましょう。
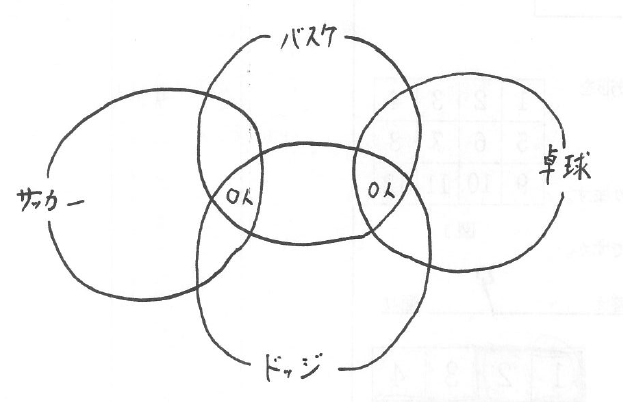
大問6 × × ×
元来は4つのベン図を図にあらわすことは出来ませんが、この問題に関しては(ア)の条件に注目することで以下のようなベン図で条件を整理することが出来ます。
ただその後の処理も条件が少なく非常に難しいので、(ウ)の「バスケットボールとドッジボールの両方に出場する生徒」を1人の時、2人の時・・・と当てはめていったほうが、現実的でしょう。
もちろん得点できなくても全く問題ありません。
このように2019年は、確実に正解すべき問題が大問1の(1)(2)(3)くらいしかなく、この数年の女子学院の出題傾向に基づいて学習を進めてきた受験生にとっては予想外の出題難度となりました。
△の問題で半分くらい得点し、合計点でも50点と少しあれば算数が原因で不合格になることはなかったものと考えられます。
2020年以降に女子学院合格を目指す受験生にとっては「基本だけでは合格は難しい、難問をじっくり考える姿勢も普段の学習を通して身につける必要がある」と改めて自覚する機会となることでしょう。

.jpg)






























