豊島岡女子学園中の算数分析（2018年 第1回）

女子トップ進学校としての確固たる地位を築いた豊島岡女子学園。

東大合格者数、医学部進学者数のいずれも非常に高いレベルを保っています。

その高い進学実績の原動力は面倒見にあると言えるでしょう。

いわゆる女子御三家と呼ばれる学校では明確な受験指導を実施しないのに対して、豊島岡女子学園の授業内容やテスト、補習は大学受験に直結します。

そのため塾に通わずにトップ大学に進学する生徒が多いことも特長です。

もちろん魅力は勉強だけではありません。

運針で得られた集中力で、文化系、運動系を問わず、多くの部が高い実績を残しています。

そんな豊島岡女子学園の中学受験は2月2日、3日、4日の3回にわたって実施されます。

特に2日の第1回の入学試験は、都内女子校トップの受験者数を誇る激戦です。

試験は算数100点、国語100点、理社が合わせて100点と、算国の比重が高いことが特徴です。

出題内容は気を衒わず、中学受験内容を高いレベルまで理解できているかを問う良問が並びます。

ここからは2018年第1回の算数の出題を通して、どうすれば豊島岡女子学園に合格を果たせるかを考えてみましょう。

2016年第1回はこちら

〇：豊島岡女子学園合格のために確実に正解したい問題

△：合否を分ける問題

×：得点できなくても、合否には影響しない問題

大問1

(1)　〇

＋のグループと、－のグループで分けて考えても良いですが、

13579-2468=11111

1357-246=1111

のように順番を組み替えたほうがスムーズに正解できるでしょう。

(2)　〇

30×□＋50×△=350÷0.7と整理しましょう。

基本的な不定方程式なので確実に正解しましょう。

(3)　〇

45以上55未満の整数なので、45から54の10個の整数の和を求めます。

こちらも落とせない問題です。

(4)　△

面積が12㎠の正方形の1辺は3cmと4cmの間となります。

3.5×3.5=12.25なので、1辺を3.5cmとすると、

20÷3.5=5.7…となり、6枚は並べられないことが分かります。

大問2

(1)　△

5×□＋4×☆=52の時、□=4か8と分かります。

また5点と4点を合わせて7問間違えて33点なので、つるかめ算より5点を5問、4点を2問間違えたと分かります。

この2つの条件を比べると、5点が4問だと条件が成り立たないので8問と導くことが可能です。

(2)　〇

Aは8秒、Bは12秒が周期になるので、24秒を調べます。

中学受験における典型題なので落とせません。

(3)　〇

面積図では捉えにくい問題です。

天秤か消去算で処理しましょう。

豊島岡女子学園を目指すなら確実に正解したい問題です。

(4)　〇

「半径の利用　⇒　二等辺三角形の利用　⇒　正三角形に気づく」という中学受験頻出パターンです。

弧の同じ長さ部分を置き換えることで、半径6cmで中心角60度のおうぎ形の弧が10個と、6cmの直線が5個と整理できます。

大問3

(1)　〇

5を和分解すると(0,0,5) (0,1,4) (0,2,3) (1,1,3) (1,2,2)になります。

あとは百の位に0が来ないことに注意して調べましょう。

(2)　△

□□□1の時、大きいほうから3桁は(1)より15通り。

□□□3の時、大きいほうから3桁の和が3なので(0,0,3) (0,1,2) (1,1,1)を調べて6通り。

□□□5の時は1005の1通りとなります。

注意深い場合分けが必要です。

大問4

(1)　△

Aさんの家から図書館をア分、図書館から公園をイ分。

Bさんの家から図書館をウ分、図書館から公園をエ分と置いてみると、

ア＋イ　　　　＝20分　…①

ア　　　　＋エ＝22分　…②

　　イ＋ウ　　＝23分　…③

と整理できます。

②＋③－①より、ウ＋エ＝25分と求められますね。

速さに見せかけた消去算です。

(2)　△

①②より図書館から公園に、ＡとＢのかかった時間の差は2分。

①③より家から図書館に、ＡとＢのかかった時間の差は3分と分かります

この比を家から図書館と、図書館から公園の距離の比と考えてみましょう。

(3)　△

Ａさんの速さを⑤m/分、Ｂさんの速さを④m/分と考えましょう。

問題の条件に合うのはＡさんとＢさんの進んだ距離の差が④となる時なので、ＡさんとＣさんが出会ったのは4分後と分かります。

大問5

(1)　△

問題の条件より、△ADEと△FBEの面積は等しくなります。

高さの比が2:1なので、底辺の比は逆比の1:2になることを利用すると、以下の図のように面積を設定することが可能です。

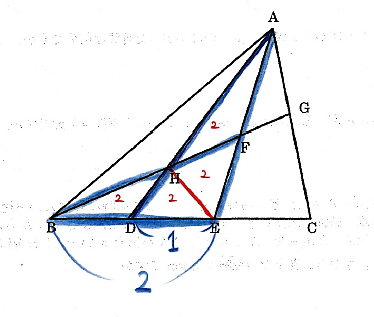(2)　△

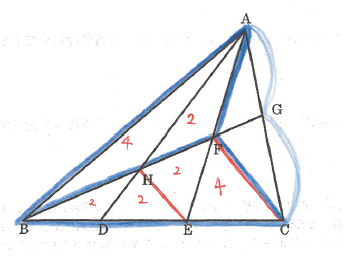
△FECの面積は(20-4-2-2-2-2)÷2より4㎠と分かります。

あとは図のように面積比と底辺の比の関係に持ち込みましょう。

大問6

(1)　△

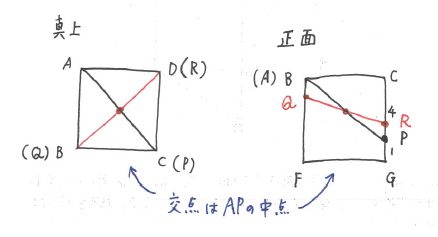
「立体図形は平面で捉える」ことが鉄則です。

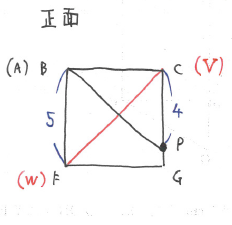
この問題では、図のように「真上から見た図」⇒「正面から見た図」の順に捉えると良いでしょう。

(2)　△

(1)より、２つの直線は必ずAPの中点で交わることが分かります。

高度な空間認識力が問われますが、豊島岡女子学園を目指すならここまで正解したいところです。

(3)　△

(1)(2)と同様、「正面から見た図」で状況を把握しましょう。

今年度も「数」「図形」「文章題」の３分野から、バランス良く出題されました。

3番以降の大問でも難度に大きな差はなく、受験生の力量を適切に測ることのできる選抜試験だったと言えるでしょう。

受験者平均点が61.27点、合格者平均点が74.75というのも昨年とほぼ同レベルで、数学科の先生方の高度な作問力が伺えます。

出題数は例年同様、大問1と2が5点×8問、大問3から6が6点×10問です。

小問ごとの難度を分類すると、〇が7問、△が11問、×は0問という構成です。

合格ラインの70点に到達するためには、〇で6/7、△で6/11が目安になりそうです。

大問3～6のうち、苦手な分野の大問でも(1)は得点し、得意な大問で完答を目指すことがポイントでしょう。

それにしても、この難度で合格者平均点が約75点と言うのは、さすが女子トップ生が集う豊島岡女子学園ですね。

この優秀な生徒達を、研究熱心で優秀な先生方が指導していくならば、この見事な進学実績も納得です。