記事を検索する
個別指導・家庭教師の自律学習サカセル
サカセルコラム
桜蔭中の理科分析（2023年） Column
Ⅰの化学計算とⅢの天体、知識問題は桜蔭でよく出ているもので、模試や塾のテキストで見慣れた問題だったと思いますが、大問Ⅳのばねはあまり見たことのないタイプの出題でした。
といっても読解と考察ができれば解ける問題でしたので、今年も知識・計算・読解・思考のすべてがチェックできる出題になっています。例年よりやや知識問題が多かったでしょうか。
しっかり勉強してきた、ある程度以上完成された子を求めてくるのが桜蔭です。今年も桜蔭らしい出題だったといえるでしょう。
中学受験化学計算の定番からの出題です。
過不足なく反応する点が表の値の中にはない/中和反応と気体発生の反応の組み合わせ問題…など、基本のレベルは超えていますが、桜蔭に向けて勉強してきた受験生にとっては慣れた問題でしょう。逆に、この問題に新鮮さを感じているようでは桜蔭に合格するのは難しいともいえます。
昆虫の知識と考察問題でした。
セミの成長過程はやや詳しい知識問題でしたが、他は基本～標準的なものでした。資料から考察する問題も難しくはなく、解きやすかったのではないかと思います。
季節についてのリード文から、月・星・金星の知識や図の見方・考え方が確認されました。特に難しいものではありませんが、勉強量と正確さが問われる出題だったと感じます。
また、お節や春の七草など伝統的な「常識」を問う問題も合わせて出題されています。一方で「太陽フレア」など最新の知識も出題され、求めている生徒像が見える出題でした。
台ばかりのしくみを考える問題は一見、とても難しそうに見えます。ただ、問われていることはさほど難しくなく、問題数も少なかったため、冷静に取り組めば負担は大きくありません。
後半の実験問題は受験生全員にとって初見の問題になり、結果を丁寧に考察する力が求められています。
大問Ⅰ～Ⅲが標準的な問題だったため、あまり時間をかけずに解き、大問Ⅳにじっくり取り組めば高得点が狙える出題だったと思います。
差のつくポイントは大問Ⅰでしょう。これを慣れた問題としてスムーズに解けたか、ひとつひとつをじっくり考えて解いたかが勝負を分けたと思われます。
知識や考え方の穴を作らず、化学計算や力学の計算はスムーズに解けるように練習しておくことが必須な学校です。
問題の分類
知：知識問題
考：思考問題
計：計算問題
問題のレベル分け
〇：絶対に取りたい
△：この中から半分以上取りたい
×：捨てても可
これは、解説いらないですね。
解答 イ、エ
水素は225でmL発生が止まっているので、ここで塩酸がすべて反応したことが分かります。
塩酸A4mL で 水素90mL 発生しているので
塩酸A□mL 水素225mL
これを求めます。
４×225/90＝10(mL)
これは桜蔭志望生にとっては慣れた問題でしょう。
解答 10(mL)
実験2より
アルミニウム0.3ｇがすべて反応すると水素が375mL発生しています。
水素が225mL発生するには
アルミニウム0.3ｇ 水素375mL
アルミニウム□ｇ 水素225mL
0.3×225/375＝0.18(g)
解答 0.18（g）
実験2より、0.3gのアルミニウムが塩酸と反応すると白い固体(塩化アルミニウム)が1.5g出来ているので
アルミニウム 0.3g 白い固体 1.5g
0.18g □g
1.5g×0.18/0.3＝0.9(g)
解答 0.9(g)
実験2 2％塩酸60mL 水素375mL
実験1 □％塩酸10mL 水素225mL
2％塩酸60mLに溶けている塩化水素を求めると
塩酸1mLの重さは1gなので
0.02×60＝1.2(g) になります。
発生した水素から実験1で反応した塩化水素を求めると
1.2×225/375＝0.72(g) となります。
これが塩酸10ｇ中に溶けているので
0.72÷10＝0.072→7.2(％)
解答 7.2(％)
塩酸と水酸化ナトリウム水溶液の混合液にアルミニウムを入れて気体の発生量を考える。
定番の問題です。
①はじめは塩酸が余っているので塩酸とアルミニウムが反応して水素発生
②水酸化ナトリウム水溶液50mLで完全中和なので、このときは水素発生しない
③その後は水酸化ナトリウム水溶液が余るようになりこれがアルミニウムと反応して水素発生
よって、水酸化ナトリウム水溶液が50mLのところで気体の発生量が0になっているV字形のグラフを探します。→カ、キ
表2を見ると、水酸化ナトリウム水溶液が0、10のときの気体の体積が420、420と続いているため、キになります。
解答 キ
アルミニウムを鉄に変えると、鉄は塩酸には反応して水素を発生しますが、水酸化ナトリウム水溶液には反応しないので、後半は気体が発生しません。
水酸化ナトリウム水溶液50mLの先の気体発生量が0ｍLになっているものを選べばよいので、エです。
解答 エ
ヒグラシの鳴き声。カナカナカナです。
コアプラスの463に載っています。チィーはニイニイゼミ、シャワシャワはクマゼミです。
解答 オ
少し珍しい問われ方ですが、ヒトの体で酸素を運んでいる管は「血管」ですね。
解答 血管
セミの育ち方。かなり詳しい知識です。
①木の幹や枝に産卵、1年目の冬はそのまま冬越し
②翌年の夏に木の幹や枝でふ化して地中にもぐる
③幼虫(土の中)で数年
④数年後の夏の朝、土から出て木の幹や枝で羽化
解答 ク→ウ→イ→エ
セミのオスが鳴くときにふるわせるのは「ウ」の腹弁です。メスには腹弁がありません。
解答 ウ
吸うのに適した口。サービス問題ですね。チョウです。
解答 エ
(1)資料1から、普及率が高い都道府県を東西で比較すればよいでしょう。
東京都・神奈川県と大阪府・滋賀県はOK
千葉県と京都府は×
選択肢の中にあるのは神奈川県と大阪府です。
解答 ウ
(2)資料2から、神奈川県と大阪府を比較すると違いはクマゼミですね。クマゼミが犯人でしょう。
解答 クマゼミ
日の出は地平線から太陽が出る瞬間の時刻です。
解答 ウ
(1)
新月の日が1日なので
上弦の月 7～8日
満月 15日
下弦の月 22～23日
図1の月は上弦の月と満月の間なので12日となります。
解答 ウ
(2)図1の月が南中するのは午後9時です。これは簡単でしょう。
解答 ク
数の子 ニシンの卵。ニシンは知らなくても魚卵だと分かればOKです。
田作り カタクチイワシを甘辛く煮たもの。これは難しいかもしれません。食べたことはあっても、名前は知らない小学生が多そうです。
かまぼこ 白身魚のすり身から出来ています。
黒豆と栗きんとんが植物なのは分かったと思いますが、田作りを知らず、植物なのかも？と思った受験生も多かったことと思います。
解答 イ、カ
(1)
すずな＝カブ、すずしろ＝ダイコン です。
解答 すずしろ
(2)
アブラナ科といえばモンシロチョウ！
解答 イ
(1) 計 ○
地球～すばる 4200兆km
1光年 9兆5000億km=9.5兆km
4200÷9.5＝442.1…→442光年
読めれば難しくない問題です。
解答 442(光年)
(2) 知 〇
彦星＝アルタイル です。
解答 アルタイル
(3) 知 △
デネブ、ベガ、アルタイルの正確な位置を覚えていないと解けません。しっかりした知識が必要です。
解答 ア、キ、ク
(4) 考 △
宵の明星(カ、オ)から、日没後最も長い時間見ることができるもの。
日没の西の地平線を考えます。
オの方が地平線からの角度が大きいので、沈むまでの時間が長くなります。
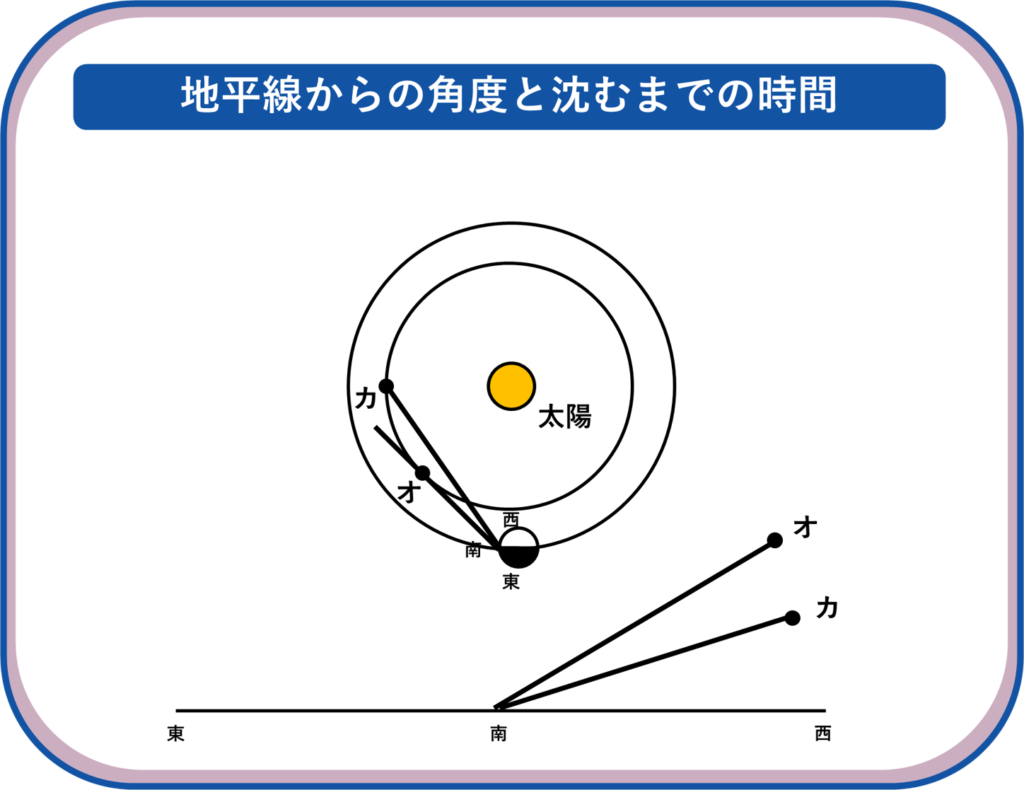
解答 オ
(5) 考 △
オは地球から見ると半分が光って見えます。(4)が出来ていれば簡単でしょう。
解答 キ
国際宇宙ステーション＝ISS(International Space Station) です。
解答 ISS
「太陽○○○」により通信障害が予想されている。「太陽フレア」です。少し詳しい知識問題です。
解答 フレア
台ばかりの使い方を考える問題です。
1 水平な台に置く
2
3 はかる物をのせる
1と3の間に入る操作は、針が「0」を指すようにする です。思いつかなかった受験生もいたかもしれません。
針の位置を調節するものを探すと、図の中に「調節ねじ」があります。
解答 a 調節ねじを回す
b 針が0を指す
ここは、難しいと感じた受験生が多かったかもしれません。
見るポイントを絞ると、さほど難しくありません。
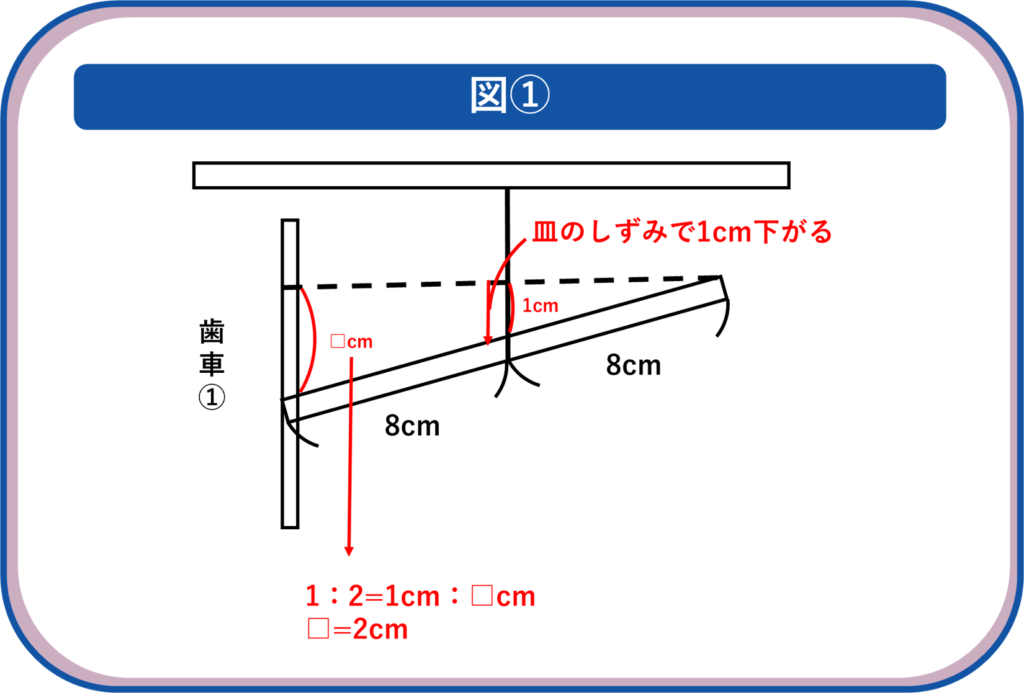
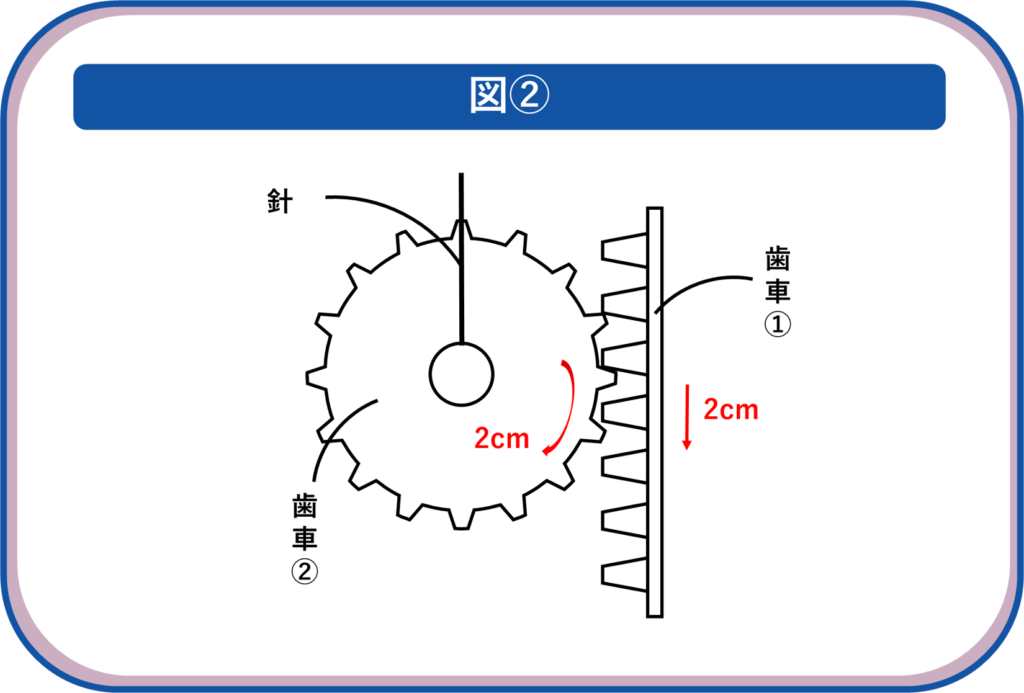
図2より、皿が1㎝下がると歯車①が2㎝下がります。
これによって歯車②が180°回転しているので
歯車②の180°分の弧が2㎝となります。
[歯車②の直径]×3.14×180/360＝2
[歯車②の直径]＝2×2÷3.14＝1.27…1.3
解答 1.3(㎝)
問3のすぐ上のリード文に「台車がPから10㎝進んだとき台車が最も速くなりました」とあるので、表1から台車の位置が10㎝になるところを探せばOKです。
| 時間(秒) | 0.6 | 0.7 |
| 位置(㎝) | 8.8 | 11.3 |
の間です。
解答 カ
11.3‐8.8＝2.5(㎝)
問3が出来ていれば簡単ですね。
解答 2.5(㎝)
ア
ゴムひもの本数同じ(1本)、引っ張ったときのゴムひもの長さ同じ(20㎝)、台車の重さ2倍はAとBの1000ですね。
| A | B | |
| 台車の重さ(g) | 500 | 1000 |
| ゴムひもの本数(本) | 1 | 1 |
| ゴムひもの長さ(㎝) | 20 | 20 |
| 0.1秒間に進んだ距離(㎝) | 2.5 | 1.7 |
0.1秒間に進んだ距離は0.5倍になっていません。
問4ができなかった場合は、Bの1000とBの1500を比較すればOKです。
台車の重さ1.5倍のとき2/3になるか確かめます。なっていません。
イ
アと同じAとBの1000を比べます。
| A | B | |
| 台車の重さ(g) | 500 | 1000 |
| ゴムひもの本数(本) | 1 | 1 |
| ゴムひもの長さ(㎝) | 20 | 20 |
| Qから進んだ距離(㎝) | 60 | 30 |
台車の重さ2倍でQから進んだ距離は0.5倍になっています。〇
ウ
AとCの40㎝を比べます。
| A | C | |
| 台車の重さ(g) | 500 | 500 |
| ゴムひもの本数(本) | 1 | 1 |
| ゴムひもの長さ(㎝) | 20 | 40 |
| 0.1秒間に進んだ距離(㎝) | 2.5 | 7.3 |
ゴムひもの長さ2倍→0.1秒間に進んだ距離2倍になっていません。
エ、オ
ゴムひもの伸びは自然長を引けばよいので、求めてみましょう。
| A | B | C | D | ||||
| 台車の重さ(g) | 500 | 1000 | 1500 | 500 | 500 | 500 | 500 |
| ゴムひもの本数(本) | 1 | 1 | 1 | 1 | 1 | 2 | 3 |
| ゴムひもの伸び(㎝) | 10 | 10 | 10 | 20 | 30 | 10 | 10 |
| Qから進んだ距離(㎝) | 60 | 30 | 20 | 240 | 540 | 120 | 540 |
A(伸び10㎝)とC(伸び20㎝)を比べる。
伸び2倍→Qから進んだ距離4倍になっています。オが〇
カ、キ
ゴムひもの本数2倍は、AとDの500gを比べます。
| A | D | |
| 台車の重さ(g) | 500 | 500 |
| ゴムひもの本数(本) | 1 | 2 |
| ゴムひもの長さ(㎝) | 20 | 20 |
| 0.1秒間に進んだ距離(㎝) | 2.5 | 3.4 |
| Qから進んだ距離(㎝) | 60 | 120 |
0.1秒間に進んだ距離は2倍になっていません。カは×
Qから進んだ距離は2倍になっています。キは〇
解答 イ、オ、キ
問5をまとめると、Qから進んだ距離は
台車の重さに反比例←イ
ゴムひもの伸びが2倍・3倍…になると4倍・9倍…(平方数倍)←オ
ゴムひもの本数に正比例←キ
となります。
Dのゴムひもの本数2本と比べます。
| D | 問6 | |
| 台車の重さ(g) | 500 | 250 |
| ゴムひもの本数(本) | 2 | 2 |
| ゴムひもの伸び(㎝) | 10 | 15 |
| Qから進んだ距離(㎝) | 120 | □ |
イより台車の重さ1/2倍→Qから進んだ距離2倍
オよりゴムひもの伸び1.5倍→Qから進んだ距離2.25倍
120×2×2.25＝540(㎝)
解答 540(㎝)
にほんブログ村にも参加しています。ぜひ下のバナーをワンクリックで応援もお願いします！
この記事を書いたのは...
齊藤弥生
指導歴 約25年
個別指導講師/家庭教師→日能研講師→個別指導講師/家庭教師
結果の確実性と生徒や一緒に組んだ算数講師に合わせる柔軟性で重宝される。
理科が好き。仕事を通して理科好きを増やすのが野望。
そのためにテストで数字を上げる、合格に導くといった仕事はそれをいちばんにしている講師以上のレベルを目指している。
個人の趣向はあるので、理科の内容自体にあまり興味が持てない子に対しては「好きではないけど点が取れる科目」を目指す。こういうものが好きな人もいるんだな、と多様性を感じてもらえればさらにうれしい。
趣味は坂巡りと買い物。坂や崖の写真を撮っているとたまに怪しまれるため、マニアな行動をするときはなるべくオシャレをして出かけます。
