早稲田中の算数分析（2018年 第1回）

日本を代表する伝統ある私立男子校の１つである早稲田中学校。

「早稲田」を名乗ったのは早稲田大学よりも先で、現在は系属校として約半数の生徒が早稲田大学に進学しています。

一方で東大や医学部への進学実績も高く、個々の生徒に応じたきめ細やかな指導は、非常に評価が高いことで知られます。

これだけの実績を残す早稲田中、当然のように中学受験においてもトップ校の一角です。

ただ出題内容は、いずれの科目も癖の強すぎないスタンダードなもの。

普段受けている模試に近い印象を受ける生徒も多いようです。

中学受験のための努力を充分に重ねてきた生徒が欲しいという考えなのでしょう。

算数においても、大問１・２は小問集合として各3題、大問３・４・５が各3題の枝問に分かれた大問の、計15問で60点満点というスタイルは不変です。

ただ難度は多少上下することが特徴として挙げられます。

合格者平均点が8割近い年度もあれば、逆に5割に満たない年度もあるので、あらかじめ目標点を決めておくことは危険です。

問題の難度を適切に見極め、正解すべき問題を確実に正解する力が求められます。

なお早稲田中は解答のみを記入する方式なので、部分点は与えられません。

「何を問われているか？」を入念に確認し、ミスを最小限に抑える意識も非常に大切です。

ここからは2018年第1回の出題を通し、どうすれば早稲田中の算数において合格ラインを越えられるかを考えていきましょう。

○：早稲田中合格のために確実に正解したい問題

△：合否の差がつく問題

×：正解できなくても合否に影響しない問題

大問1

(1)　△

あまり目にしない問題設定ですが、実質は普通のニュートン算です。

線分図でまとめても良いですし、

□÷(2－赤)=5分

□÷(3－赤)=3分

など式で整理しても良いでしょう。

(2)　△

おまけの消しゴムは当然ながら無料なので、まずは不定方程式として条件を整理しましょう。

30×□＋50×△=940

より(□,△＋おまけ)=(3,17) (8,14＋1) (13,11＋2) (18,8＋3) (23,5＋4) (28,2＋5)と調べられたら、あとは互いに素ではないものを選びましょう。

(3)　△

早稲田中で稀に見られる推理の問題です。

出題頻度は決して多くは無いものの、条件の与え方が巧みです。

この問題ではAが3人追い抜く必要があるので4位以下、Gが4位と与えられているので、もともと5位か6位と分かります。

あとはEB○○Dと、C○○Aの両方が成り立つ場合を調べましょう。

答える際はゴールした順番であることにも気を付けましょう。

大問2

(1)　○

半径が与えられていない扇形は中学受験においては定番です。

四分円＋半円－直角二等辺三角形と読み替え、確実に正解したい問題です。

(2)　△

円を転がす問題も典型題です。

ただこの問題はやや処理量が多いので注意が必要です。

直線部分と曲線部分を丁寧に区別して考えましょう。

最終的には直線部分が30cmと曲線部分が240度ぶんになります。

(3)　△

水の量と空気の量が変わらないことに注目しましょう。

12.8:2.2=64:11なので、図のように考えてみると解きやすいでしょう。

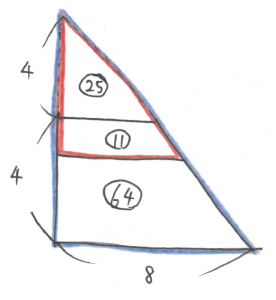
正面から見た面積の比が36：100＝9：25なので、

相似比は3：5と考えられますね。

大問3

(1)　○

ボールの跳ね上がりも、中学受験においては散見されるテーマです。

図の比率が非常に極端で解きにくいものの、順に計算するだけなので易しいでしょう。

(2)　△

左と右の両方から求められる高さを記入していきます。

Cの台の高さを□とすると、

137＋41－□：70＋35－□＝２：１

と整理出来ます。

(3)　△

(2)で正解できれば易しいでしょう。

丁寧に戻っていくと、与えられた図のような状況になって安心できたのではないでしょうか。

大問4

(1)　○

早稲田中らしい、比を上手く活用させる通過算です。

連結部1ヶ所を①mとすると、

(220＋⑩＋320＋⑮)÷(普通＋貨物)＝14秒

(220＋⑩＋320＋⑮)÷(普通－貨物)＝70秒

電車の長さの和は同じなので、時間の比の14：70＝1：5の逆比が、電車の速さの和：電車の速さの差、と考えられます。

シンプルに「距離が一定だから時間と速さが逆比」と考えて正解したい問題です。

(2)　△

普通列車の速さを[3]貨物列車の速さを[2]とすると、

(220＋⑩＋320＋⑮)÷([3]－[2])＝70秒

(220＋⑩＋220＋⑩)÷([3]－[2])＝57秒

あとは丁寧に消去算として式を処理していきましょう。

(3)　△

(2)が正解できれば易しい問題です。

普通列車は228mで24m/秒、貨物列車は16m/秒なので

普通列車が渡り終えるのは(1500＋228)÷24＝72秒後になります。

あとは丁寧に計算しましょう。

大問5

(1)　△

以下のように三角形の相似に注目していくと

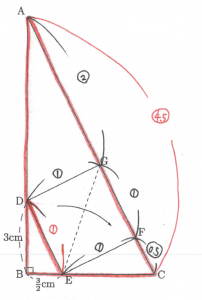
△ABCと△DBEの相似比が4.5：1＝9：2と分かります。

ここから面積比で考えてみましょう。

なお以下のように三角形を組み合わせて考えても良いでしょう。

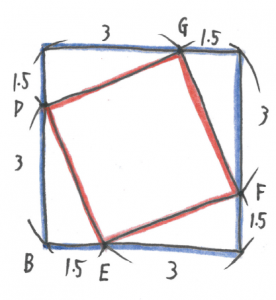
(2)①　×

対応関係に気づきにくい難問です。

(1)で直角三角形の相似に気づけていたら、与えられた図に2つの二等辺三角形を見つけることが出来るでしょう。

(2)②　×

①が出来たら丁寧に計算をするだけの問題ですが、ここまでたどり着ける受験生は少ないのかもしれません。

今年度の第1回は時間をかけずに正解できる問題が非常に少ない、厳しい試験になりました。

受験者平均点で23.0/60、合格者平均点でも33.1/60というのは、かなり低めの基準です。

出題の内訳は、○が3問、△が、/10問、×が/2問なので、

合格のためには○で3/3問、△で5/10問、×で0/2問の合計8/15問が目安になりそうです。

たしかに早稲田中は図形の出題数が多く難度が高いことが特徴です。

ただ比と割合の文章題や速さと比など、他の分野も中学受験内容を逸脱しない中で、質の高い難問が課されます。

来年以降に早稲田中を目指す皆さんは、まずは通っている塾のテキストに掲載されている問題のうち、典型的な難問まで頑張って学習しましょう。

6年生の後半からは過去問を通して、問題の取捨選択やミスを防ぐための取り組みに力を入れられると良いですね。

明確な対策が立てにくいぶん、日頃の頑張りが結果につながっていきますよ。